- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
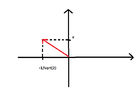
A force $6N$ forms an angle $\frac{\pi}{4}$ with the y-axis, showing to the right.
The force is opposed by the movement of an object along the line that connects $(1,2)$ with $(5,4)$.
I want to find a formula for the vector-force $F$.
The line that connects $(1,2)$ with $(5,4)$ is $l(t)=(1,2)+t(4,2), t \in \mathbb{R}$.
How can we find the formula of the force?
A force $6N$ forms an angle $\frac{\pi}{4}$ with the y-axis, showing to the right.
The force is opposed by the movement of an object along the line that connects $(1,2)$ with $(5,4)$.
I want to find a formula for the vector-force $F$.
The line that connects $(1,2)$ with $(5,4)$ is $l(t)=(1,2)+t(4,2), t \in \mathbb{R}$.
How can we find the formula of the force?