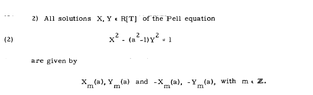How can we show that all the solutions are given by X_m(a), Y_m(a) ?

[mathmari]

Hey!

Let $F$ be an integral domain with characteristic $2$. Let $a\in F[t]$ and $a \notin F$. Let $\alpha (a)$ be a root of the equation $x^2+ax+1=0$. We define two sequences $X_m(a), Y_m(a) \in F[t], m \in \mathbb{Z}$ by
$$X_m(a)+\alpha (a)Y_m(a)=(\alpha (a))^m=(a+\alpha (a))^{-m} \tag 1$$

Lemma.
Let $F$ be an integral domain with characteristic $p=2$. Let $a \in F[t], a \notin F$. For all $m, n \in \mathbb{Z}$ we have :

1. $X_m(a)$ (resp. $Y_m(a)$) is equal to the polynomial obtained by substituting $a$ for $t$ in $X_m(t)$ (resp. $Y_m(t)$).
   The degree of the polynomial $X_m(t)$ is $m-2$, if $m \geq 2$.
   The degree of the polynomial $Y_m(t)$ is $m-1$, if $m \geq 2$.
   $X_{-m}=X_m(a)+aY_m(a)$
   $Y_{-m}(a)=Y_m(a)$
   
2. All solutions $X, Y \in F[t]$ of the equation $$X^2+aXY+Y^2=1\tag 2$$ are given by $X_m(a), Y_m(a)$, with $m \in \mathbb{Z}$.

I want to prove this lemma but I am facing some difficulties at $2$.

First I showed that $(X_m(a), Y_m(a))$ is a solution of the equation $(2)$. But how could we show that all the solutions of the equation $(2)$ are given by $X_m(a), Y_m(a)$.

I have no idea how to do that... Could you give me some hints?

 

[mathmari]

At the paper that I am looking I found the corresponding lemma for the case that the characteristic is not $2$ and its proof:

View attachment 4804
View attachment 4805

PROOF.

View attachment 4806
View attachment 4807I want to try to do the same for the case $\text{char}=2$ but first I have to clarify some points at the proof above. Why do we suppose that $R$ (in our case $F$) is an algebraically closed field?

Why do we consider the field $K=R(t)(a)$?

Is $S$ the set of points at which the functions of $K$ are not defined?

 

[mathmari]

$$X^2+aXY+Y^2=1$$

We set $X=x$ and $Y=2y$. Then we have $$x^2+2axy+4y^2=1 \Rightarrow x^2+2axy+a^2y^2-a^2y^2+4y^2=1 \Rightarrow (x+ay)^2-(a^2-4)y^2=1$$

So we have to find the solutions of an equation of the form $$p^2-ks^2=1$$

Since we are working in a field of characteristic $p=2$ and since $k=a^2-4$, does it stand that $k=a^2$ ?