How Can You Prove BC^2 Equals BK Times BQ in Equilateral Triangles?

[anemone]

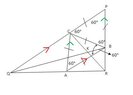
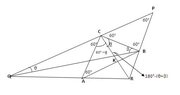
$P,\,Q,\,R$ is a triangle. $A,\,B,\,C$ lie on the sides $QR,\,RP,\,PQ$ respectively so that $PBC$ and $ABC$ are equilateral. $QB$ and $RC$ meet at $K$.

Prove that $BC^2=BK\cdot BQ$.

---

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[anemone]

No one answered last week's problem.:(

You can find the solution below:

Spoiler

View attachment 4107

$QCA$ and $ABR$ are similar triangle (since the sides are parallel) so we have

$\dfrac{QC}{CA}=\dfrac{AB}{BR}$ or

$\dfrac{QC}{CB}=\dfrac{CB}{BR}$ since $CA=CB$ and $AB=CB$.

Notice also that $\angle QCB=\angle CBR=120^{\circ}$ so triangles $QCB$ and $CBR$ are similar hence $\angle CQB=\angle BCR$.

Hence, $BC$ is tangent to the circle $CQK$ hence $BC^2=BK\cdot BQ$.

 

[anemone]

Hi MHB,

I received a PM asking for clarification regarding the last line in the above solution, so I think there is a need for me to offer clarification publicly on that point, after all, MHB is a place to ask questions when you aren't sure about something in any given solution and our POTW does hold to that principle completely.(Sun)

Thanks for reading and I do apologize if my previous reply is less than completely clear.

Spoiler

View attachment 4112

After we have found out that $\angle CQB=\angle BCR$ and if we let it as $\theta$, we notice from triangle $QCB$ that

$\theta+\beta+120^{\circ}=180^{\circ}$

This gives $180^{\circ}-(\theta+\beta)=120^{\circ}$

Apply Sine Rule on triangles $QBC$ and $KBC$ respectively, we see that

$\triangle QBC$: $\dfrac{BC}{BQ}=\dfrac{\sin \theta}{\sin 120^{\circ}}$

$\triangle KBC$: $\dfrac{\sin \theta}{\sin (180-(\theta+\beta))^{\circ}}=\dfrac{BK}{BC}$ $\rightarrow \dfrac{\sin \theta}{\sin 120^{\circ}}=\dfrac{BK}{BC}$

$\therefore \dfrac{BC}{BQ}=\dfrac{BK}{BC}$, i.e. $BC^2=BK\cdot BQ$.