- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
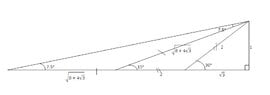
Prove that $\cot 7\dfrac{1}{2}^{\circ}=\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{6}$.