arhzz
- 283
- 57
- Homework Statement
- Find the voltage and current in the circuit
- Relevant Equations
- General math
Hello!
Disclaimer: I am not really sure in which forum I should post this problem since the homework is electrical engineering,but the problem I am facing is of mathematical nature (at least I think).
Consider this circuit;
The given RC network contains the resistors R1 = 200 Ω and R2 = 300 Ω
and the capacitance C = 50 µF and is obtained by closing the ideal switch S
applied to the DC voltage U = 10 V at t = 0
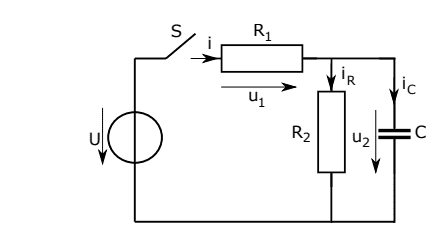
a)Determine i(t) and u2(t).
Now I've solved problems like this,and it always involes solving a inhomogenous differential equation. First I've used Kirchoffs law and ## i(t) = i_r(t)+ i_c(t) ## We can write the current through the resistor and coil like this;
## i(t) = \frac{u_2(t)}{R_2} + C \frac{du(t)}{dt} ## Now using second kirchhoffs law I get that the voltage ## u_2 = U - R_1i(t) ## where R1 times I is the voltage at the first resistor.
And now here is where I am having problems. I was not really able to move ahead of this part but looking at the solutions these are the steps and I do not understand them very well.
"Plugging in the loop equation in the node equation"
## i(t) = \frac{U}{R_2} - \frac{R1}{R2}i(t) - R_1 C \frac{di(t)}{dt} ##
Now I think I get this step; I am assuming that for some reason they split up the first fraction since it should be ## \frac{U-R_1i(t)}{R2} ## but that should be equal to what they have written. For the second part If we plug it in we get ## C \frac{d(U-R_1i(t)}{dt} ## and if I derive this it should be ## 0 - R_1i(t) ## and after some simplifying I get the the same equation like in the book. Now assuming I've understood this step,this one has got me completely stumped.
"and from this the differential equation"
## \frac{di(t)}{dt} + (\frac{1}{R_1} + \frac{1}{R_2})*\frac{1}{C} i(t) = \frac{U}{R_1R_2C} ##
I really don't see how they get from the step before to this step. Now assuming its simply math I am really baffeled,maybe I am missing something in terms of the circuit analysis although the problems I did before were pretty much straight forward after using the Kirchoffs laws.
Thanks for the help,and excuse the long post!
Disclaimer: I am not really sure in which forum I should post this problem since the homework is electrical engineering,but the problem I am facing is of mathematical nature (at least I think).
Consider this circuit;
The given RC network contains the resistors R1 = 200 Ω and R2 = 300 Ω
and the capacitance C = 50 µF and is obtained by closing the ideal switch S
applied to the DC voltage U = 10 V at t = 0
a)Determine i(t) and u2(t).
Now I've solved problems like this,and it always involes solving a inhomogenous differential equation. First I've used Kirchoffs law and ## i(t) = i_r(t)+ i_c(t) ## We can write the current through the resistor and coil like this;
## i(t) = \frac{u_2(t)}{R_2} + C \frac{du(t)}{dt} ## Now using second kirchhoffs law I get that the voltage ## u_2 = U - R_1i(t) ## where R1 times I is the voltage at the first resistor.
And now here is where I am having problems. I was not really able to move ahead of this part but looking at the solutions these are the steps and I do not understand them very well.
"Plugging in the loop equation in the node equation"
## i(t) = \frac{U}{R_2} - \frac{R1}{R2}i(t) - R_1 C \frac{di(t)}{dt} ##
Now I think I get this step; I am assuming that for some reason they split up the first fraction since it should be ## \frac{U-R_1i(t)}{R2} ## but that should be equal to what they have written. For the second part If we plug it in we get ## C \frac{d(U-R_1i(t)}{dt} ## and if I derive this it should be ## 0 - R_1i(t) ## and after some simplifying I get the the same equation like in the book. Now assuming I've understood this step,this one has got me completely stumped.
"and from this the differential equation"
## \frac{di(t)}{dt} + (\frac{1}{R_1} + \frac{1}{R_2})*\frac{1}{C} i(t) = \frac{U}{R_1R_2C} ##
I really don't see how they get from the step before to this step. Now assuming its simply math I am really baffeled,maybe I am missing something in terms of the circuit analysis although the problems I did before were pretty much straight forward after using the Kirchoffs laws.
Thanks for the help,and excuse the long post!