How Do Angular and Linear Velocities Relate in Cyclist Work-Energy Problems?

[simphys]

Homework Statement

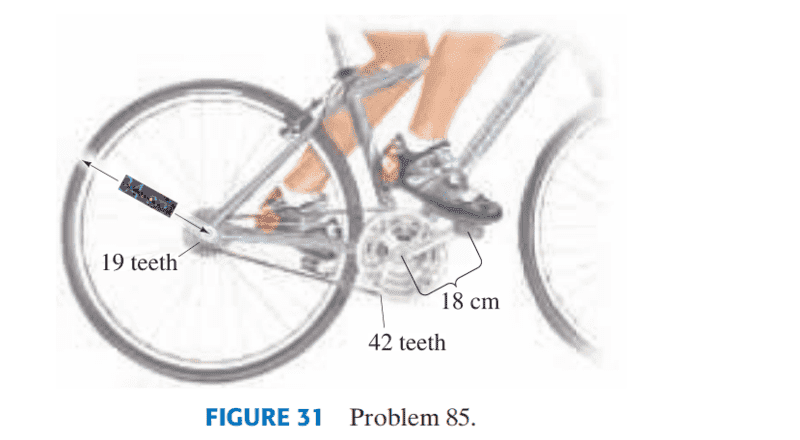
85. Assume a cyclist of weight mg can exert a force on the
pedals equal to 0.90 mg on the average. If the pedals rotate
in a circle of radius 18 cm, the wheels have a radius of 34 cm,
and the front and back sprockets on which the chain runs
have 42 and 19 teeth respectively (Fig. 31), determine the
maximum steepness of hill the cyclist can climb at constant
speed. Assume the mass of the bike is 12 kg and that of the
rider is 65 kg. Ignore friction. Assume the cyclist’s average
force is always: (a) downward; (b) tangential to pedal motion.

Relevant Equations

work-energy

can I get some tips on how to approach this problem ? I don't get where I should start on this one.
thank you

 

[BvU]

can I get some tips on how to approach this problem ? I don't get where I should start on this one.
thank you

Hi,

As you should know by now, PF guidelines require you to at least attempt to start a solution and post that.
The key in this exercise is the transfer of torque from pedal wheel end to real axle. Write some equations to convert the $0.9 \ mg$ to a torque, equate torque on the two axles and then convert the torque to a force.

What force is needed to climb a slope of $\theta$ at constant speed ?

 

[Delta2]

Basically your task is to find how the force of 0.90mg that is used to rotate the pedals, is "transferred" as force F between the rear wheel and the road that makes the bike move (pretty much like F=ma).

In order to find how this transferring is done you got to find some torques:

The torque of the 0.90mg force to the front pedal, which (given that the bike is moving with constant speed, hence also everything is rotating with constant angular velocity which means angular acceleration is zero) equals the torque of the force from chain in the front sprocket, find the force from chain in the first sprocket, then find the torque of this force in the back sprocket (the forces from chain in the front and back sprocket are equal in magnitude) and then equate this last torque to the torque from the friction from the road to the rear wheel and hence find the friction force which will be the force F I talked about in the first paragraph. And then I guess you can do the rest.

 

[Delta2]

Hmm now I see you have this as work energy problem. Yes I think it can be done without the concept of torque. Is this how you supposed to do it, without the concept of torque?

Anyway for the case a) where the force is always downward is easy. Find the work in one rotation of the pedal and from it calculate the average force tangential to the incline and from it the slope of the hill. It is a trivial case that's why it is easy (work and force have a trivial value).

 

[haruspex]

Start with case b. Case a worries me.. either it's a trick question or the poser has overlooked something.

 

[Halc]

determine the maximum steepness of hill the cyclist can climb at constant speed. ...
Assume the cyclist’s average force is always: (a) downward

Case a) has no answer of course. When the pedals are at the top/bottom, zero torque is being applied and the bicycle will slow on the hill, violating the constant speed requirement.

OK, they probably mean constant average speed over each rotation of the pedals, but even then the answer is speed dependent since at high speed the average time spent at any given part of the rotation is fairly similar, but at really low speed, a far greater percentage of the time is spent at the low-torque portion of the effort, changing the average torque applied over time.

Doing from a work perspective seems the way to go. The torque perspective might work better for case b.

 

[Delta2]

Start with case b. Case a worries me.. either it's a trick question or the poser has overlooked something.

Yes it seems like a trick question, but I think the poser wants us to consider the instantaneous speed approximately constant. There is acceleration in half the cycle and deceleration in the other half of cycle, average acceleration should be zero.

 

[haruspex]

There is acceleration in half the cycle and deceleration in the other half of cycle

Seems to me it's in quarter cycles, alternating faster and slower.

 

[Delta2]

Seems to me it's in quarter cycles, alternating faster and slower.

Quarter cycles? Why?? Anyway the work of the force in one complete cycle is zero (I hope we won't disagree about that) so no kinetic energy added to the bike in one cycle so the slope must be..

 

[haruspex]

Quarter cycles? Why?? Anyway the work of the force in one complete cycle is zero (I hope we won't disagree about that) so no kinetic energy added to the bike in one cycle so the slope must be..

One cycle is a complete rotation of the crankshaft. The torque is low either side of the vertical arrangement of the pedals, which occurs twice per cycle.

 

[Delta2]

One cycle is a complete rotation of the crankshaft. The torque is low either side of the vertical arrangement of the pedals, which occurs twice per cycle.

Yes the torque will be zero twice per cycle (and maximum twice per cycle too), I still don't understand why we will have quarter cycles of acceleration-deceleration.

 

[Delta2]

The way I understand the torque changes sign twice per cycle and not four times per cycle.

 

[haruspex]

The way I understand the torque changes sign twice per cycle and not four times per cycle.

It doesn't change sign at all. The legs take it in turn to push. (If cleats were used it would be the tangential force case.) It goes like $|\cos(\theta)|$, so two maxima and two minima per cycle.

 

[Delta2]

It doesn't change sign at all. The legs take it in turn to push. (If cleats were used it would be the tangential force case.) It goes like $|\cos(\theta)|$, so two maxima and two minima per cycle.

Sorry you got me totally confused, let's start to clear some of the confusion, $\theta$ is the slope of the hill or $\theta=\omega t$??

 

[Orodruin]

Sorry you got me totally confused, let's start to clear some of the confusion, $\theta$ is the slope of the hill or $\theta=\omega t$??

The latter. Once one pedal reaches the bottom, you shift the weight to the other pedal, thus maintaining driving torque throughout the cycle.

 

[Delta2]

The latter. Once one pedal reaches the bottom, you shift the weight to the other pedal, thus maintaining driving torque throughout the cycle.

I am not so sure the problem wants us to view it that way but yes ok that is what happens when we do bike.

 

[haruspex]

I am not so sure the problem wants us to view it that way but yes ok that is what happens when we do bike.

What other way would make sense? If the torque keeps changing sign you'll go nowhere.

 

[simphys]

@haruspex @Delta2 @Orodruin

First of all, my apologies for not mentioning that it is viewed as a 'translation' kinetic energy problem.

Delta2 is right. It only considers translation kinetic energy in this chapter that's why I got a little bit confused as I thought it might refer to rotational motion being that there's a ratio b/n the torques dependent on the radii between the back and front sprockets. We didn't study rotational motion(besides moments/torques in static situations I assume because the center of mass is involved in rot motion) yet at university but I'll get there after linear momentum.

I am thus not completely understanding the view in terms of the torque but I'll look back it in a couple of days.
For the translation KE-work point of view:
So how can I go from knowing the average force he can exert on the pedals onto the getting what the max steepness is going to be?
I can potentially calculate the work done by the cyclist on the pedals and find a relation between the weight of the cyclist and the slope? as it'll be the only force acting if the system is considered as a whole.

Thanks in advance

 

[simphys]

Hi,

As you should know by now, PF guidelines require you to at least attempt to start a solution and post that.
The key in this exercise is the transfer of torque from pedal wheel end to real axle. Write some equations to convert the $0.9 \ mg$ to a torque, equate torque on the two axles and then convert the torque to a force.

What force is needed to climb a slope of $\theta$ at constant speed ?

my apologies you are right, I didn't really know where to start and had already done quite a lot of exercises so wasn't really on top of my game aka becoming a bit lazy to figure it out I guess..

 

[simphys]

that's really about it, I can't find any relation to be honest.. totally stuckk...

 

[Delta2]

Ok now we know you can't use the torque concept but only work energy force concepts. So in my opinion what you should do is:

1. Find the work the cyclist does in one rotation of the pedals $W_1$
2. Find how much the rear wheel moves in one rotation of the pedals. The front and rear sprocket ratio and the rear wheel radius will feature in this (as well as the radius of the pedals)
3. Let $W_2=Fx$ is the work of the hypothetical average force F that makes the bike move (translational motion), where x the distance from 2. Equate $W_1=W_2$ and solve for F
4. Solve a typical 1 body problem in an incline where you have the weight of the bike+rider, the force F and the normal reaction from the incline. The force F will be parallel to the incline.

 

[haruspex]

my apologies for not mentioning that it is viewed as a 'translation' kinetic energy problem.

I.e., ignore rotational KE? I don't think anyone on the thread supposed we had tonconsider that. It is a constant; once established, no further work needs to be done to maintain it.

The main part of the task is to use the info re radii and tooth counts to figure out the mechanical advantage. Don’t worry about forces until you have done that.

 

[simphys]

Ok now we know you can't use the torque concept but only work energy force concepts. So in my opinion what you should do is:

1. Find the work the cyclist does in one rotation of the pedals $W_1$
2. Find how much the rear wheel moves in one rotation of the pedals. The front and rear sprocket ratio and the rear wheel radius will feature in this (as well as the radius of the pedals)
3. Let $W_2=Fx$ is the work of the hypothetical average force F that makes the bike move (translational motion), where x the distance from 2. Equate $W_1=W_2$ and solve for F
4. Solve a typical 1 body problem in an incline where you have the weight of the bike+rider, the force F and the normal reaction from the incline. The force F will be parallel to the incline.

thank you!
one question: for 2. is it correct that to get the ratio I need to consider the fact that the angular velocity of both sprockets and then simply equate them?
oh and for 3. why do I assume W_1 = W_2?
4. I did that as first a first step indeed. But then the exact relationships you described in 1,2,3 were a bit unclear so thank you for that once again.

 

[simphys]

I.e., ignore rotational KE? I don't think anyone on the thread supposed we had tonconsider that. It is a constant; once established, no further work needs to be done to maintain it.

The main part of the task is to use the info re radii and tooth counts to figure out the mechanical advantage. Don’t worry about forces until you have done that.

Well.. me neither to be honest :'d
Yep got it, I doesn't seem difficult, thanks a lot! I guess once I understand rotational motion it'll be even more clear.

 

[Delta2]

thank you!
one question: for 2. is it correct that to get the ratio I need to consider the fact that the angular velocity of both sprockets and then simply equate them?

The sprockets have different angular velocity but same linear velocity (because they are connected by a chain). The back sprocket and the rear wheel have same angular velocity but different linear velocity.

oh and for 3. why do I assume W_1 = W_2?

You assume that because we assume that all the energy the cyclist puts, goes into translational kinetic energy of the rider+bike system. $W_2$ will be equal to the Kinetic energy of the rider+bike.

 

[simphys]

The sprockets have different angular velocity but same linear velocity (because they are connected by a chain). The back sprocket and the rear wheel have same angular velocity but different linear velocity.

You assume that because we assume that all the energy the cyclist puts, goes into translational kinetic energy of the rider+bike system. $W_2$ will be equal to the Kinetic energy of the rider+bike.

my apologies.. yep I meant the omega thing in rev/s(angular velocity thus appearantly) is different due to the radii, and Linear vel is constant which forms the relationship between the two angular velocities

for the 2nd. Oh okay got it thank you. That's epic i.e. I can thus simply see this as forming the relation between rotational motion and translation motion