- #1
parttime
- 13
- 0
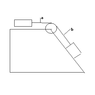
there are two blocks on a trapizoid one on the top and one on the side with the slope a wire that goes throu a pully connects the two. determin the the acceleration of the two blocks.
block one =m1 block two = m2 pully =m with radius r Ufriction =.36
what i have so far is
sum of forces(along x axis) on block one is t (for tension) - ufm1g=m1a(acceleration)
sum of forces (along yaxis) on block two is tsin(thata) +ufm2gsin-mg=m2a
is this correct
block one =m1 block two = m2 pully =m with radius r Ufriction =.36
what i have so far is
sum of forces(along x axis) on block one is t (for tension) - ufm1g=m1a(acceleration)
sum of forces (along yaxis) on block two is tsin(thata) +ufm2gsin-mg=m2a
is this correct