Elara04
- 5
- 0
- Homework Statement
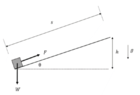
- An object on an inclined plane of weight W=20kN is acted on by a force of 10.1 kN parallel to an inclined plane. The object travels up the slope at a constant speed and travels over a distance s = 37 m, also gaining h = 9 m in height.
How much work is done against friction (i.e. energy dissipated as heat)? Give your
answer in kilo-joules (kJ)
- Relevant Equations
- 𝑊 = 𝐹 ∙ ∆ 𝑠 = 𝐹 ∥ ∆ 𝑠
I'm unsure on where to begin with this question, i've tried many different formulas that aren't giving me the right answer. I believe to start I need to convert the kilo newtons to newtons.
I tried w = fs + mgh
w = 10500 x 8.9/sin(13.9)+(1845.69 x 9.8 x8.9) = 549986.46 J
and then convert to kilo joules = 549.99 kJ
But this isn't correct
any help would be appreciated
I tried w = fs + mgh
w = 10500 x 8.9/sin(13.9)+(1845.69 x 9.8 x8.9) = 549986.46 J
and then convert to kilo joules = 549.99 kJ
But this isn't correct
any help would be appreciated