How do I calculate the ratio of forces between two conducting spheres?

[samcoelho]

Homework Statement

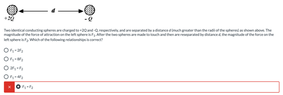
Two identical conducting spheres are charged to +2Q and -Q, respectively, and are separated by a distance d (much greater than the radii of the spheres) as shown above. The magnitude of the force of attraction on the left sphere is F1. After the two spheres are made to touch and then are reseparated by distance d, the magnitude of the force on the left sphere is F2. Which of the following relationships is correct?

Relevant Equations

Coulomb's Law: F=k|q1q2|/r^2

Here are the answer choices:
a) F₁ = 2F₂
b) F₁ = 8F₂
c) 2F₁ = F₂
d) F₁ = 4F₂
e) F₁ = F₂

I figured that Coulomb's law would tell us the magnitude of the forces are identical, so I answered E, but that was incorrect.

(Screenshot of question attached)

 

[Steve4Physics]

After the spheres touch, how much charge is on each?

 

[tech99]

If the magnitude of the forces was unequal, we could use this experiment to propel a space vehicle.

 

[haruspex]

If the magnitude of the forces was unequal, we could use this experiment to propel a space vehicle.

You seem to have misread the question.

 

[samcoelho]

After the spheres touch, how much charge is on each?

Equal amount, so does each sphere then have 1/2 Q charge?

 

[Steve4Physics]

Equal amount, so does each sphere then have 1/2 Q charge?

Yes, well done.

The total charge is (2Q) + (-Q) = Q. Since the spheres are identical, this total charge gets split equally, $\frac Q 2$ each.

 

[rude man]

Yes, well done.

The total charge is (2Q) + (-Q) = Q. Since the spheres are identical, this total charge gets split equally, $\frac Q 2$ each.

Equal amount, so does each sphere then have 1/2 Q charge?

Good.
Now finish off. What are the before & after forces?