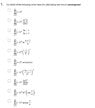How Do I Correctly Apply the Alternating Series Test?

In summary, a series is a sum of a sequence of numbers written in the form of Σan. Convergence refers to the behavior of a series as the number of terms approaches infinity, and a series is considered to converge if the sum of its terms approaches a finite number. There are two types of convergence, absolute and conditional, and a convergence test is used to determine which type a series has. The choice of convergence test depends on the properties of the series and it may be necessary to try multiple tests to determine convergence.
  • #1
chrisgoodie
1
0
View attachment 5930

Hi guys, I am doing this question of alternating series test.

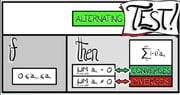
And I was following the below principles when solving the problem. Sorry I don't know how to type in the math language. I got 4, 8, 9, 10 as the answers. But the system rejected this without any explanation. Can someone throw a lifeline?

View attachment 5931
View attachment 5932
 

Attachments

  • WeChat_1472482813.jpeg
    WeChat_1472482813.jpeg
    62.2 KB · Views: 81
  • 1.pic.jpg
    1.pic.jpg
    40.4 KB · Views: 87
  • 2.pic.jpg
    2.pic.jpg
    39.5 KB · Views: 75
Physics news on Phys.org
  • #2
Hey chrisgoodie! Welcome to MHB! ;)

How about this one:
$$\sum_{n=1}^\infty (-1)^n \left( \frac{3n-1}{n^2} \right)^n$$
(Wondering)
 

FAQ: How Do I Correctly Apply the Alternating Series Test?

What is a series?

A series is a sum of a sequence of numbers. It can be written in the form of Σan, where n is the number of terms in the sequence and an is the nth term.

What is convergence?

Convergence refers to the behavior of a series as the number of terms approaches infinity. A series is considered to converge if the sum of its terms approaches a finite number as n increases.

What is the difference between absolute convergence and conditional convergence?

A series is said to have absolute convergence if the series of absolute values of its terms converges. If the series of absolute values diverges but the original series still converges, it is said to have conditional convergence.

What is the purpose of a convergence test?

A convergence test is used to determine whether a series converges or diverges. There are various tests that can be used, such as the ratio test, the comparison test, and the integral test.

How do I know which convergence test to use?

The choice of convergence test depends on the specific properties of the series. It is important to carefully consider the terms of the series and choose a test that is appropriate for the given situation. It may also be helpful to try multiple tests and compare the results.

Similar threads

I Unable to show the radius of convergence of a numeric series
Replies
8
Views
2K
I Infinite Series - Divergence of 1/n question
Replies
5
Views
447
I How does the ratio test fail and the root test succeed here?
Replies
6
Views
2K
MHB Does the Comparison Test Determine Convergence or Divergence of Series?
Replies
3
Views
1K
I Alternating Series, Testing for Convergence
Replies
4
Views
1K
Can an alternating series with decreasing terms converge to zero?
Replies
6
Views
1K
MHB Which test do we have to apply at each case?
Replies
6
Views
2K
Alternative examples, alternating series test
2
Replies
40
Views
4K
MHB Series Convergence Or Divergence
Replies
1
Views
1K
MHB Power Series (Which test can i use to determine divergence at the end points)
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top