- #1
Biochemgirl2002
- 30
- 1
Moved from technical forum so no template
The question
Sometimes road surfaces have banked curves, use a FBD to explain how it helps cars make turns more safely My trial:
I drew this FBD (attached below)
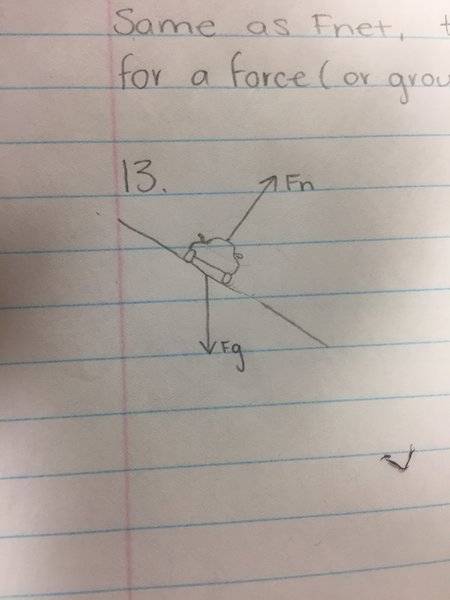
And I think it helps make driving more safe because the Fn acting on the car is pointed more towards the middle of the curve, which acts as a centripetal force. Which like in space, where centripetal force acts as your gravity, the centripetal force will cause the car to stick to the road and not slip as much Does this sound correct? How can I elaborate more?
Sometimes road surfaces have banked curves, use a FBD to explain how it helps cars make turns more safely My trial:
I drew this FBD (attached below)
And I think it helps make driving more safe because the Fn acting on the car is pointed more towards the middle of the curve, which acts as a centripetal force. Which like in space, where centripetal force acts as your gravity, the centripetal force will cause the car to stick to the road and not slip as much Does this sound correct? How can I elaborate more?
