How do I evaluate the integral for a specified area on the xy-plane?

[Petrus]

Hello MHB,
This is an exemple I do not understand.
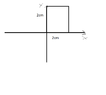
if $$R={(x,y)|-1 \leq x \leq 1, -2 \leq y \leq 2}$$, evaluate the integral
$$\int\int_R \sqrt{1-x^2}dA$$ (It is suposed to be R at down for 'rectangle' if I understand correct.)
they solve it like this $$\int\int_R \sqrt{1-x^2}dA = \frac{1}{2} \pi(1)^2 * 4 = 2\pi$$
I don't understand how they do it and
The defination says:
"If $$f(x,y) \geq0$$, then the volume V of the solid that lies above the rectangle R and below the surface $$z=f(x,y)$$ is
$$V=\int\int_R f(x,y)dA$$"
What I can note is that $$\sqrt {1-x^2} \geq0$$ and $$z=\sqrt{1-x^2} <=> x^2+z^2=1$$ so then the volume lies above the rectangle and below $$z= \sqrt{1-x^2}$$ but I get confused with dA, integrate respect to area?

Regards,

 

[alyafey22]

You are asked to solve the integral

$$\int^{2}_{-2} \, \int^{1}_{-1} \sqrt{1-x^2} \, dx \, dy$$

 

[Petrus]

You are asked to solve the integral

$$\int^{2}_{-2} \, \int^{1}_{-1} \sqrt{1-x^2} \, dx \, dy$$

is it that easy >.<

 

[alyafey22]

Yes , you are asked to integrate over the rectangle [-1,1]x[-2,2]

 

[Petrus]

Yes , you are asked to integrate over the rectangle [-1,1]x[-2,2]

How will it work with integrate with dy? I don't have any y in my function so..?

 

[alyafey22]

You can think of it as a nested integral so you start first by evaluating $$\int^1_{-1} \sqrt{1-x^2} \, dx $$

Then what ever the result you get assume to be f(y) then you evaluate

$$\int^{2}_{-2} f(y) \, dy $$

 

[Petrus]

You can think of it as a nested integral so you start first by evaluating $$\int^1_{-1} \sqrt{1-x^2} \, dx $$

Then what ever the result you get assume to be f(y) then you evaluate

$$\int^{2}_{-2} f(y) \, dy $$

Thanks Zaid!:) One last quest why can I do that? I don't think I ever read about it or I have just missed it. Thanks!

 

[alyafey22]

This is what we call iterated integral .

- - - Updated - - -

Just as an exercise try to evaluate the integral of z=2 over the rectangle [0,2]x[0,2] and verify this is the volume of a cube.

 

[Petrus]

This is what we call iterated integral .

- - - Updated - - -

Just as an exercise try to evaluate the integral of z=2 over the rectangle [0,2]x[0,2] and verify this is the volume of a cube.

This is what makes this forum so good:)! Thanks for helping me and giving me an exercise! I really like this thanks thanks!:)

we got :
$$\int_0^2\int_0^22 dxdy$$ so the volume becomes $$V=8cm^3$$ (I just like to have 'unit'
A cube is like 6 square View attachment 736 when our is 2cm long (Here is me draw it on paint but it looks like a rectangle but its a square) View attachment 737 formel for volume of a cube is $$a^3$$ and our $$a=2$$ ( lenght) so the volume of the cube becomes $$2^3=8cm^3$$

 

[alyafey22]

Excellent , so we see that for positive z>0 this is actually the volume over the specified area on the xy-plane .