How do I find cos and sin values without a calculator?

[Casio1]

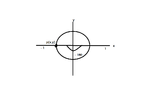
Please refer to the diagram.

I am asked to find cos - 180⁰ and sin -180⁰ by plotting a point p on a circle.

OK I don't understand the following before I begin to answer.

How do I know where to start to draw the circles?

I have the x and y axis. I know that anti-clockwise rotation is positive and clockwise is negative.

If I look first at cos - 180⁰

I know I am going to draw a semi circle in the clockwise direction, which will represent 180⁰ but show as - 180⁰ on the diagram.

I am confused how I draw the sin -180⁰ and am assuming that I draw the semi circle in a anti-clockwise direction labelled also - 180⁰ to end up with a circle.

I also don't understand from a drawing how I am supposed to know that cos - 180⁰ = - 1, and sin - 180⁰ = 0

From first principles and not looking at the calculator, how would I know that these values are right, I could have drawn the semi-circles from x = 2 or 3 etc?

Please advise if you can.

Kind regards

Casio

 

[SuperSonic4]

For simplicity use the unit circle (radius=1) in your diagrams
I'd use parametric equations in this case to split your axes into $x = \cos(t) \text{ and } y = \sin(t)$.

You've correctly put point P on the graph so what is the value of x at -180? What about y? The values will be equal to $\cos(-180)$ and $\sin(-180)$ respectively.

 

[Casio1]

For simplicity use the unit circle (radius=1) in your diagrams
I'd use parametric equations in this case to split your axes into $x = \cos(t) \text{ and } y = \sin(t)$.

You've correctly put point P on the graph so what is the value of x at -180? What about y? The values will be equal to $\cos(-180)$ and $\sin(-180)$ respectively.

As I am just learning this from first principles my foundation understanding of the subject is a little unstable at the moment, so I would like to keep things as simple as possible if I we can. Parametric equations might be getting a little too involved just at the moment thanks.

So referring to what you advise above and in conjunction with the diagram, point P is positioned at - x, the point would be using your idea of the radius = 1 being cos - 180⁰ = - 1

The y-axis or y value when x = - 1 must be that y = 0 with reference to the diagram.

So in conclusion;

cos - 180⁰ = - 1, and sin - 180⁰ = 0

Thanks

Casio(Smile)

 

[SuperSonic4]

As I am just learning this from first principles my foundation understanding of the subject is a little unstable at the moment, so I would like to keep things as simple as possible if I we can. Parametric equations might be getting a little too involved just at the moment thanks.

So referring to what you advise above and in conjunction with the diagram, point P is positioned at - x, the point would be using your idea of the radius = 1 being cos - 180⁰ = - 1

The y-axis or y value when x = - 1 must be that y = 0 with reference to the diagram.

So in conclusion;

cos - 180⁰ = - 1, and sin - 180⁰ = 0

Thanks

Casio(Smile)

Parametric equations is a fancy way of splitting the x and y axes into components. It enables you to say that whatever the x value is then that is equal to the value of $\cos(t)$ (t is just a variable) and the y value is $\sin(t)$

In this case because P is at (-1,0) then $\cos(-180) = x$ and $\sin(-180) = y$

Without knowing what you've studied so far it's hard to suggest a method of working out. For example you (can) use the unit circle to prove periodicity so you can't say that $\sin(-180) = \sin(-180+360)$. Have you covered even and odd functions (see spoilers for what I mean)

Spoiler

• An even function is where $f(-x) = f(x)$. Examples are $f(x) = x^2$ and, more thematically appropriate $f(x) = \cos(x)$
• An odd function is where $f(-x) = -f(x)$. Examples include $f(x) = x^3$ and $f(x) = \sin(x)$

You'd use these functions to say that $\cos(-180)= \cos(180)$ and work out the positive angle

 

[Casio1]

Parametric equations is a fancy way of splitting the x and y axes into components. It enables you to say that whatever the x value is then that is equal to the value of $\cos(t)$ (t is just a variable) and the y value is $\sin(t)$

In this case because P is at (-1,0) then $\cos(-180) = x$ and $\sin(-180) = y$

Without knowing what you've studied so far it's hard to suggest a method of working out. For example you (can) use the unit circle to prove periodicity so you can't say that $\sin(-180) = \sin(-180+360)$. Have you covered even and odd functions (see spoilers for what I mean)

Spoiler

• An even function is where $f(-x) = f(x)$. Examples are $f(x) = x^2$ and, more thematically appropriate $f(x) = \cos(x)$
• An odd function is where $f(-x) = -f(x)$. Examples include $f(x) = x^3$ and $f(x) = \sin(x)$

You'd use these functions to say that $\cos(-180)= \cos(180)$ and work out the positive angle

Hi, yes very briefly but a lot of revision to do on it to get a solid foundation.

Kind regards

Casio