clhrhrklsr
- 23
- 0
View attachment 2879
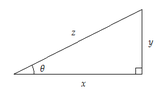
Someone please take a look at the attachment above. These two questions have me stumped and it ask on each question to find three missing angles. I don't even know where to start. Could someone be so kind and explain to me how to figure each of these. I need help with this asap to help my studying of trigonometry and geometry. Thanks
Someone please take a look at the attachment above. These two questions have me stumped and it ask on each question to find three missing angles. I don't even know where to start. Could someone be so kind and explain to me how to figure each of these. I need help with this asap to help my studying of trigonometry and geometry. Thanks