- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How Do I Find P1 and P2 for a Parametrized Curve?
- Thread starter Niall101
- Start date
-
- Tags
- Curve
In summary, the conversation discusses the process of finding P1 and P2 in order to satisfy a given equation, using a slanted ladder as an example. The speaker suggests finding a and b in terms of x, L, and λ, and using trig functions of θ. They plan to continue working on this after class.
Physics news on Phys.org
- #2
- 9,568
- 775
You don't want to start with the general equation of a conic because you don't know ahead of time it even is a conic. I know, the question tells you that, but you shouldn't assume it.
Here's a picture of the slanted ladder:
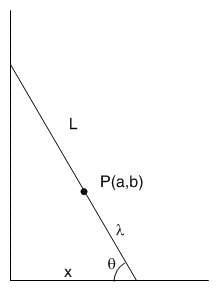
Figure out a and b in terms of x, L, and λ. You will need to use the trig functions of θ which you can also get in terms of x, L, and λ. That should get you started.
Here's a picture of the slanted ladder:
Figure out a and b in terms of x, L, and λ. You will need to use the trig functions of θ which you can also get in terms of x, L, and λ. That should get you started.
- #3
Niall101
- 20
- 0
Thanks so much! I am going to work more on this today after class.
FAQ: How Do I Find P1 and P2 for a Parametrized Curve?
What is a parametrized curve?
A parametrized curve is a mathematical concept that represents a curve in a coordinate system by using a set of parameters. These parameters can be any mathematical expression or variable, and they help to define the position, direction, and shape of the curve.
How is a parametrized curve different from a regular curve?
A regular curve is typically defined by an equation in terms of x and y coordinates, while a parametrized curve is defined in terms of parameters. This means that a parametrized curve can represent more complex curves that cannot be easily expressed in terms of x and y coordinates.
What is the purpose of finding a parametrized curve?
Finding a parametrized curve allows us to describe and analyze complex curves in a more efficient and accurate way. It also helps in solving various problems in mathematics, physics, and engineering, where curves are involved.
How do you find the parametrized curve of a given equation?
The process of finding the parametrized curve of a given equation involves identifying the parameters and finding a set of equations that express the curve in terms of those parameters. This can be done by manipulating the given equation and solving for the parameters.
What are some real-life applications of parametrized curves?
Parametrized curves have various real-life applications, such as in computer graphics for creating smooth and realistic curves, in physics for describing the motion of particles, in engineering for designing and analyzing complex structures, and in economics for modeling demand and supply curves.
Similar threads
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 14
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 7
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 4
- Views
- 5K
Share: