katerowe
- 7
- 0
- Homework Statement
- From a force time graph. Normal force is (18.20 ± 0.01) . I need to find μstatic and μkinetic. I also need to find uncertainties
- Relevant Equations
- μstatic = F,ax static / F normal
μkinetic = F friction/ F normal
I have found that μstatic= 5.6 (found on graph) / 18.20 = 0.3077
I don't know how to find Force of friction from the graph to calculate μKinetic
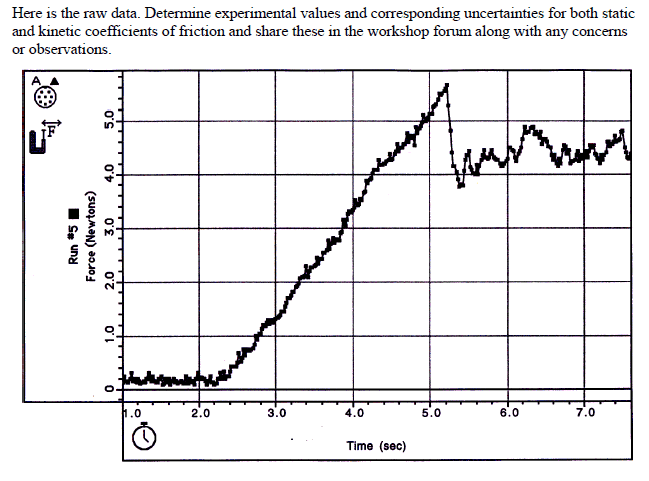
I don't know how to find Force of friction from the graph to calculate μKinetic
Attachments
Last edited by a moderator: