How do I find the force in each member?

In summary, the conversation discusses how to determine the forces in each member of a truss and whether they are in tension or compression. The suggested method is to use trigonometry to calculate angles, sum forces in the y direction and moments about a point to solve for reaction forces, and then use free body diagrams to find internal forces. There is also a discussion about setting up equations for joints with multiple unknowns and how to solve for them using the sum of forces in x and y. Additionally, there is a clarification on collinear members and the importance of taking into account all three members attached to a joint when solving for internal forces.
  • #1
shreddinglicks
216
6

Homework Statement


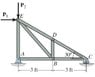
Determine the force in each member of the truss. State if the members are in tension or compression.
P1 = 450 lb, P2 = 600 lb

Homework Equations

The Attempt at a Solution


No matter what I try I get wrong answers. I need someone to get me going in the right direction.
 

Attachments

  • Hibbler.ch6.f6_new.jpg
    Hibbler.ch6.f6_new.jpg
    8.5 KB · Views: 1,656
Physics news on Phys.org
  • #2
First use trigonometry to calculate all the angles of the triangles, then sum the forces in the y direction and sum the moments about point a to solve for your reaction forces at a and c. then you can make cuts around different joints and do free body diagrams to solve for all the internal forces.

Edit: also sum the forces in the x-direction to solve for the reaction force in the x direction at a
 
Last edited:
  • #3
CodyZim said:
First use trigonometry to calculate all the angles of the triangles, then sum the forces in the y direction and sum the moments about point a to solve for your reaction forces at a and c. then you can make cuts around different joints and do free body diagrams to solve for all the internal forces.

Edit: also sum the forces in the x-direction to solve for the reaction force in the x direction at a

How do I sum the forces in the y direction when I only know one of the forces, the 600 lbs?
 
  • #4
I did the torque about A. M = -450(3.46)+Fc(6)

used:
tan(30) = 0pp./6

to get 3.46 ft.

M = 259.5 ft*lb
 
  • #5
shreddinglicks said:
How do I sum the forces in the y direction when I only know one of the forces, the 600 lbs?
Sum the moment about point A and set equal to zero to get an equation in terms of only the y reaction at point C.
 
  • #6
shreddinglicks said:
I did the torque about A. M = -450(3.46)+Fc(6)

used:
tan(30) = 0pp./6

to get 3.46 ft.

M = 259.5 ft*lb
259.5 is the value of the force at C in the y direction not the torque(Torque is the same as moment)

Knowing that, sum the forces in the y direction and solve for point a
 
  • #7
This is the work done so far, thanks in advance you have been great help.

My last question, how do I find the force at BE?
 

Attachments

  • CCI11132014.jpg
    CCI11132014.jpg
    30.6 KB · Views: 785
  • #8
shreddinglicks said:
This is the work done so far, thanks in advance you have been great help.

My last question, how do I find the force at BE?
Looks like you need to set up the equations for the joints B, D, and E. You'll have three unknowns: Fbd, Fbe, and Fde. You'll also have enough equations to plug in for and solve for them. It won't be as analytic as finding the other joints, but it will work. If you need help with that or any more further explaining let me know
 
  • #9
CodyZim said:
Looks like you need to set up the equations for the joints B, D, and E. You'll have three unknowns: Fbd, Fbe, and Fde. You'll also have enough equations to plug in for and solve for them. It won't be as analytic as finding the other joints, but it will work. If you need help with that or any more further explaining let me know

I'm confused since CD and DE are collinear they both have the value of 519lb. DB is 0 because it is part of a collinear member. So isn't my only unknown BE?
 
  • #10
shreddinglicks said:
I'm confused since CD and DE are collinear they both have the value of 519lb. DB is 0 because it is part of a collinear member. So isn't my only unknown BE?
Give me a second I'll work the math out really quickly.
 
  • #11
CodyZim said:
Give me a second I'll work the math out really quickly.
Your joint D math is incorrect, you still have to take into account that there are three members, and you have to include DE in your x and y calculations

If you set up equations in the x and y for points B, D, and E, you should have three unknowns and three equations, and be able to solve for them. Each point has two trusses that are unknown. Just because CD and DE are colinear does not mean they are the same value. Only if there was no point in between then with a truss going down would they be equal to each other always
 
  • #12
CodyZim said:
Your joint D math is incorrect, you still have to take into account that there are three members, and you have to include DE in your x and y calculations

If you set up equations in the x and y for points B, D, and E, you should have three unknowns and three equations, and be able to solve for them. Each point has two trusses that are unknown. Just because CD and DE are colinear does not mean they are the same value. Only if there was no point in between then with a truss going down would they be equal to each other always

Could you elaborate? I want to make sure I understand this. The answer key says CD and DE are equal, and going by my notes it says collinear members are equal.

As far as setting up a systems, Basically you are saying to take my x and y of each point and combine them so I get 3 equations?
 
  • #13
What he is saying is that you need to take in account all three members attached to joint D because we have three internal forces compressing or in tension around joint D. Draw a FBD of joint D with all the internal forces around it. If only know one internal force you can make a system of equations to solve for the two unknowns. Sum of the forces in x and sum of the forces in y to make the two equations.
 
Last edited:
  • #14
ME_student said:
What he is saying is that you need to take in account all three members attached to joint D because we have three internal forces compressing or in tension around joint D. Draw a FBD of joint D with all the internal forces around it. If only know one internal force you can make a system of equations to solve for the two unknowns. Sum of the forces in x and sum of the forces in y to make the two equations.
^ This
Just sum the x and y direction for points B,D, and E. you won't be able to solve for the internal sections with just one point. you need to set up multiple equations and solve in terms of one force, and plug that into another equation
Example:

Lets say you solve for the x and y in point B and get
Fbe = Fbc - Fbd (these are just theoretical values, NOT the actual answer)

Solving point d, we'd get:
Fdb = Fde + 2*Fdc

Solving Point E gives:
Fed = Fea + Feb + 450

You know Fbc, Fdc, and Fea. Other than that, just plug one value in and solve for the three values with the three equations
 
  • #15
So you can find Fed and Feb with a system of equations, but you need to solve for bata and alpha
 

Attachments

  • pic1.pdf
    80.2 KB · Views: 408
  • #16
I did end up getting the answer. Thanks guys for putting in the time to help me.
 

FAQ: How do I find the force in each member?

1) How do I calculate the force in each member of a structure?

The force in each member of a structure can be calculated using Newton's third law of motion, which states that for every action, there is an equal and opposite reaction. This means that the force acting on a member will be equal to the force exerted by that member on the structure. By analyzing the external forces acting on the structure and using the equations of static equilibrium, the force in each member can be determined.

2) What factors affect the force in each member of a structure?

The force in each member of a structure is influenced by several factors such as the type of load (point load, distributed load, etc.), the geometry and dimensions of the structure, the support conditions, and the material properties of the members. Other factors like temperature, wind, and seismic forces may also affect the force in each member.

3) Can the force in each member of a structure change over time?

Yes, the force in each member of a structure can change over time due to various factors such as changes in external loads, structural modifications, and material degradation. This is why it is important to regularly inspect and monitor structures to ensure that the force in each member is within safe limits.

4) How can I visualize the force in each member of a structure?

One way to visualize the force in each member of a structure is by creating a free body diagram for each member. This diagram will show all the external forces acting on the member, as well as the internal forces within the member. Another way is by using structural analysis software, which can provide detailed visualizations of the forces in each member.

5) What happens if the force in a member exceeds its capacity?

If the force in a member exceeds its capacity, it can result in structural failure, which can lead to serious consequences. Therefore, it is crucial to ensure that the force in each member is within the safe limits determined by structural design codes and standards. If the force in a member is found to be too high, it may be necessary to make structural modifications or use stronger materials to increase its capacity.

Similar threads

How Do You Calculate Distributed Load on a Roof Truss Due to Snow?
Replies
3
Views
4K
Calculate Force Member in Truss
Replies
2
Views
2K
Finding Forces in Member AE & AB: Exam Follow-up
Replies
1
Views
2K
Engineering Resultant Force and Direction using Parallelogram Law
Replies
6
Views
2K
Checking My Work: Solving for Force in Member GH
Replies
3
Views
1K
Statics - Compression and tension forces in a truss
Replies
2
Views
6K
Truss Method of Joints: Solving Unequal Member Forces
Replies
2
Views
2K
How Do You Calculate Forces in Truss Members?
Replies
1
Views
1K
How do I determine the force in each member of the truss?
Replies
4
Views
3K
Optimized "4 Zero Force Members: Check If You Have It Right
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top