- #1
Poirot1
- 245
- 0
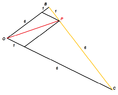
Let B=(5,21), C=(40,-14) and $\frac{BP}{PC}$=1/6. What is the most efficent way to find P? My book just states P=(6/7)B+(1/7)C but no idea how they got that.