How do I find the the total Resistance?

[MePhysica]

Hello,

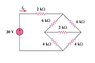
This is a little basic I know, but I'm a little confused on how I would calculate the total resistance for this circuit... this circuit was actually to find I0 using mesh analysis, but I was trying to figure out the resistance to obtain I0 using ohms law. I am not sure how to incorporate the 2kΩ into the calculations.. (I was thinking it was something like 2+(((6||6)||2)||(4||4)) )

Can anyone help?

Thanks!

 

[Studiot]

Hello mephysica, welcome to physics forums.

Is this homework or schoolwork?

Are you sure you mean 'mesh analysis'?, not some other theorems?

What difference would removing the 2k resistor make to i₀?

 

[MePhysica]

Hello mephysica, welcome to physics forums.

Is this homework or schoolwork?

Are you sure you mean 'mesh analysis'?, not some other theorems?

What difference would removing the 2k resistor make to i₀?

Thanks for the reply!

Yes it was homework, The actual question was "For the bridge network, find I0 using mesh analysis."
The actual solving of this was pretty straightforward, solving 3 simultaneous equations to obtain i0 = i1 = 4.286 mA using KVL.

But my question was how to analyze the resistors in this configuration- and removing the 2k would mean the overall R is reduced... so from V = IR, the current would be reduced?

 

[Studiot]

I realized after that there are two 2k resistors.

So I am referring to the one across the "bridge" formed by the 6k and 4k resistors.

What do you mean by mesh analysis? What equations did you use?

Clearly the resistance load experienced by the 30 volt source is given by 30/i₀.

You have correctly calculated i₀.

Now to understand this circuit what is the current through the 2k resistor across the bridge and why?

 

[MePhysica]

I'm not sure if the term "mesh analysis" is not a popular term internationally, but generally it's looking at the "closed loops" and forming the equation based on Kirchhoff's Voltage Law, namely:
(assuming the big loop is i1, and the smaller loops are i2, and i3 respectively)
Equation 1, mesh 1: 30 = 12i1 - 6i2 -4i3
Equation 2, mesh 2: 0 = -6i1 + 14i2 - 2i3
Equation 3, mesh 3: 0 = -4i1 - 2i2 + 10i3
And solving those equations, i0 = i1 = 4.286mA

I'm not too sure what the current is across the 2kΩ resistor on the bridge... would it be 0, since the current perhaps bypasses it?

 

[Studiot]

OK, that's fine we are getting somewhere.

I will return to terminology at the end and concentrate on your resistance question first.

Let us call the 2k resistor R6.

Now R6 can be any value you like and it will make no difference to the result since there is no current in it.

There is no current in it because both ends are at the same voltage. ie there zero voltage across it.

That is why I originally suggested you remove it, since it actually plays no part in the circuit.

If we remove it you have two branches comprised of a 6k in series with a 4k fed from the same voltage nodes.

So the resistance of this is (6k+4k) || (6k+4k) = 5k.

This is in series with the first 2k resistor call it R1.

So the total resistance = 2k + 5k = 7k

So i₀ = 30/7000 ≈ 4.5 mA as you calculated.

Can you follow this so far?

 

[MePhysica]

Ah right! The potential difference is 0.. Completely forgot about that

Yeah it totally makes sense now. Thanks for walking me through it!

 

[Studiot]

Good that we got that sorted.

Now for some terminology, that should be of interest to a keen computer student.

Electric circuits, by their nature, form loops or circuits.

These loops can be analysed by various methods, some of which work directly on the currents and voltages actually applied to the components.

The use of Kirchoff's two laws KVL and KCL is such a method.
This leads to a set of simultaneous linear equations you obviously know well how to solve.

Notice that I have used the term loop (Kirchoff's original term) not mesh.

This is because there is another method, developed before KVL/KCL by Maxwell, called Maxwell's mesh method.

Maxwells method (he originally used the term mesh) requires one fewer equation that KCL methods and obviously leads to the same results.

However it does not deal directly with the actual currents flowing.
It assigns an imaginary current to each loop in the mesh ( a mesh is a set of conjoined loops) which is the same throughout that loop.

The actual results are derived from the set of solutions to Maxwells mesh equations for these fictious currents.
This method lends itself particularly well to formal computer analysis of electrical power networks.

 

[MePhysica]

This is because there is another method, developed before KVL/KCL by Maxwell, called Maxwell's mesh method.

Maxwells method (he originally used the term mesh) requires one fewer equation that KCL methods and obviously leads to the same results.

However it does not deal directly with the actual currents flowing.
It assigns an imaginary current to each loop in the mesh ( a mesh is a set of conjoined loops) which is the same throughout that loop.

The actual results are derived from the set of solutions to Maxwells mesh equations for these fictitious currents.
This method lends itself particularly well to formal computer analysis of electrical power networks.

Hmm, I don't think the term "Maxwell's mesh" was explicitly stated, but what you described is what I used to derive the formulas 30 = 12i1 – 6i2 – 4i3 where – 6i2 – 4i3 would be the result of the other meshes on the loop.

But again, thanks for the explanation.

 

[Studiot]

Since you didn't define i1, i2 or i3 it is hard to tell. However if you did not apply actual currents and voltages to the resistors then you did not use Kirchoff.

Another small point, you should post this type of question in the homework section, according to the rules here.

Perhaps next time?