xyz_1965
- 73
- 0
Good morning everyone. I'm working on some right-triangle trigonometry problems in the Cohen textbook as I wait to receive my Sullivan precalculus book. It should arrive next week.
Suppose that theta = 39.4° and x = 43.0 feet. Find h and round answer to one decimal place.
I found h to be 27.3 feet.
The gable is the triangular region bounded by the rafters and the attic floor. Find the area of the gable. Round the final answer to one decimal place.
Before calculating the area, I needed to find the radius, which turns out to be 33.2 feet.
I then used A = (1/2)(base)(height).
My answer is 906.4 ft^2.
The book's answer is 906.9 ft^2.
How do I get the book's answer?
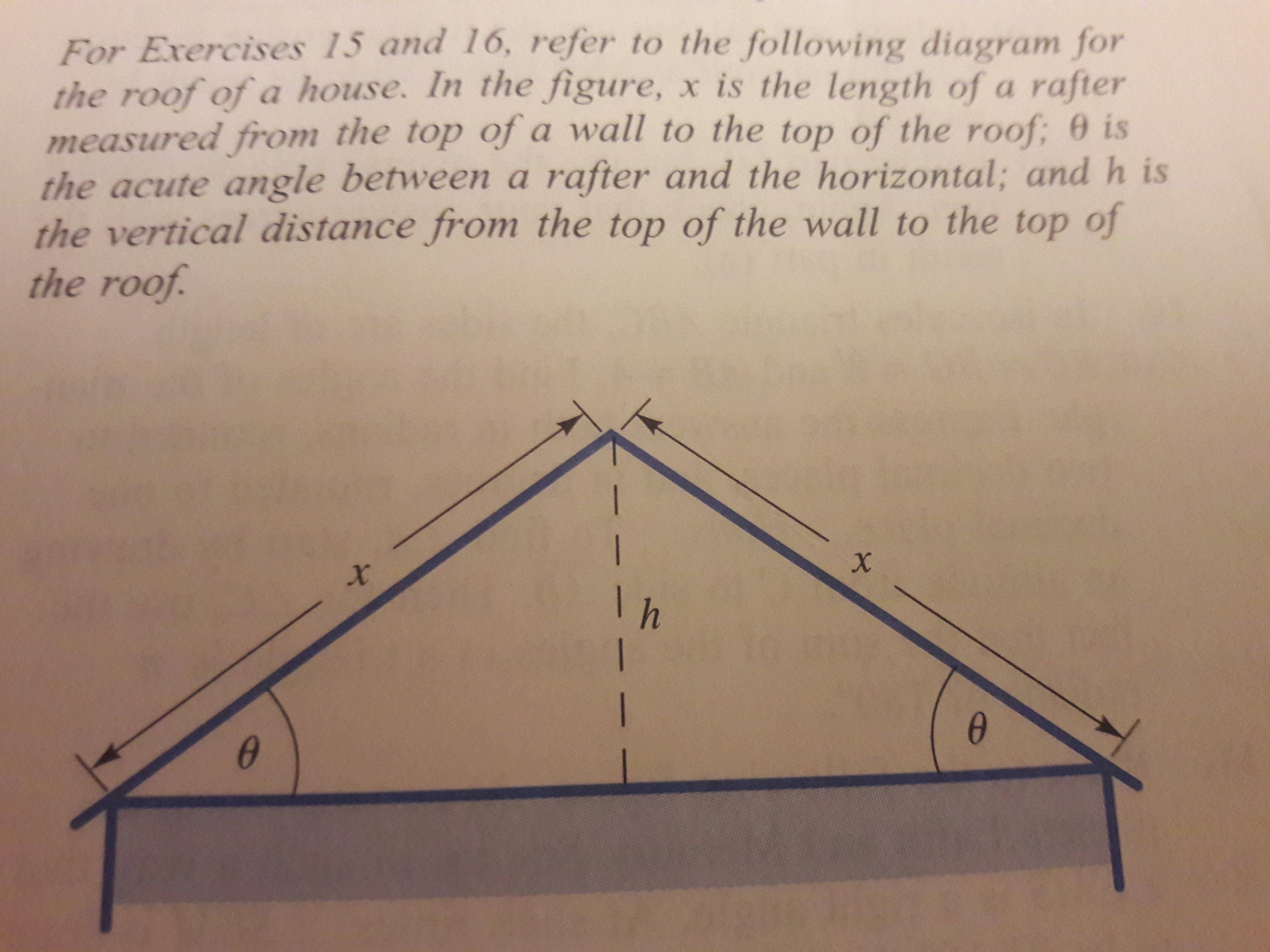
Suppose that theta = 39.4° and x = 43.0 feet. Find h and round answer to one decimal place.
I found h to be 27.3 feet.
The gable is the triangular region bounded by the rafters and the attic floor. Find the area of the gable. Round the final answer to one decimal place.
Before calculating the area, I needed to find the radius, which turns out to be 33.2 feet.
I then used A = (1/2)(base)(height).
My answer is 906.4 ft^2.
The book's answer is 906.9 ft^2.
How do I get the book's answer?