samlag
- 2
- 0
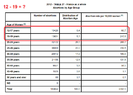
- I would like to find the 12 to 19 abortion rate per 10,000 women from the following table:
This would be the merging of age groups "12-17" with "18-19" to some how get the 12-19 abortion rate.
EDIT: "Distribution of abortion age" was translated from "Répartition des ges l'avortement" in French. It appears to me to be the percentage each age group's abortions are of the total amount of abortions.
The answer I came up with is 125.67 per 10,000. Not sure if that is correct.
I multiplied the rate per individual woman by the number of abortions for each group which I think gave the number of women. I added both of these groups together. I added both groups number of abortions and then divided the amount of women by amount of abortions and multiplied it by 10,000.
If you would like to answer, its probably best to focus on the math, and not politics :)
Attachments
Last edited: