- #36
pete
- 72
- 5
I don’t really understand some of the terminology you use, the sum of the force on the upper wall, that’s the numbers I get from doing the first class lever calculation? And the applied force, that’s the number I get from doing the second class lever calculation I guess?
And everything summing to zero. The walls will always be stronger than the clamp so won't the force always sum to zero? I don’t know how to apply an equation with acceleration to a static object. You talk about acceleration a lot and I really don’t understand what you mean when everything if fixed in place.
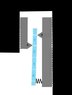
It’s good that the drawing looks OK, was it not a problem that the numbers for the two walls are different, I though they had to be equal? That’s the summing to zero bit?
And everything summing to zero. The walls will always be stronger than the clamp so won't the force always sum to zero? I don’t know how to apply an equation with acceleration to a static object. You talk about acceleration a lot and I really don’t understand what you mean when everything if fixed in place.
It’s good that the drawing looks OK, was it not a problem that the numbers for the two walls are different, I though they had to be equal? That’s the summing to zero bit?