- #1
thatguy14
- 45
- 0
Homework Statement
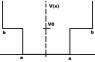
The question is attached as a picture. Note: if someone would prefer I type it out I can.
Homework Equations
Schrodingers equation
The Attempt at a Solution
PART A
I am pretty sure I got the well right. It looks like a finite well inside an infinite well. I have attached a crudely drawn one called "well.png".
PART B
So I know that because the potential well is even (symmetric about 0) we can choose the eigenfunctions to have some definite parity. Then since we are dealing with bound states where the energy levels are non-degenerate. Then can we say that the lowest state should always be of even parity and every alternating state should be even also? and the ones inbetween are odd? Does this apply to the entire well? I'm not sure I understand this
PART C
This is where I lose all confidence in what I know. So there are 2 cases, one where E < V0 and E > V0. For the E<V0 the solutions would look exactly like the finite well but with the added restriction that the probability of the particle being at b must be 0. For E> V0 I am not really sure... It must be bound right? But how does it behave with the drop in potential?
I'll leave it there for now. Any help would be greatly appreciated