How Do Perturbation Equations Affect FRW Cosmology Metrics?

[ergospherical]

Homework Statement

$T^{00} = a^{-2} \bar{\rho}(1+\delta)$
$T^{0i} = a^{-2} \bar{\rho}(1+w)v^i$
$T^{ij} = a^{-2} \bar{\rho} [(1+\delta)\delta^{ij} - h^{ij}]$

Relevant Equations

$\nabla_{\mu} T^{\mu \nu} = 0$

The perturbed line element: $g = a(\tau)^2[-d\tau^2 + (\delta_{ij} + h_{ij})dx^i dx^j]$
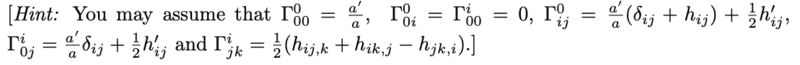
Expanding the covariant derivative with $\nu = 0$, you get a few pieces. Here on keeping only terms linear in the perturbations,

$\partial_{\mu} T^{\mu 0} = a^{-2} \bar{\rho} \left[ \delta' - 2\mathcal{H} (1+\delta) + (1+w) i\mathbf{k} \cdot \mathbf{v} \right]$

here $\mathcal{H} = a'/a$ and $i \mathbf{k} \cdot \mathbf{v} = \partial_i v^i$. Then

$\Gamma^{\mu}_{\mu \rho} T^{\rho 0} = a^{-2} \bar{\rho} \left[ 4\mathcal{H}(1+\delta) + \frac{1}{2} h' \right]$

$\Gamma^{0}_{\mu \rho} T^{\mu \rho} = a^{-2} \bar{\rho} \left[ \mathcal{H}(1+\delta)(1+3w) + \frac{1}{2} w h' \right]$

Overall,
$0 = a^{-2} \bar{\rho} \left[ \delta' + 3(1+w) \mathcal{H}(1+\delta) + (1+w) i \mathbf{k} \cdot \mathbf{v} + \frac{1}{2}(1+w)h'\right]$

but the term $3(1+w) \mathcal{H}(1+\delta)$ shouldn't be there. I can't see why not? For reference, the connection coefficients