How Do Stoichiometric Coefficients Affect Reaction Rates?

[Master1022]

Homework Statement

For the reaction the following stoichiometric coefficients have been determined: 2 $C$ react to form 2 $E$ and 1 $F$. The rate of formation of E is $1.6 \times 10^{–4} mol L^{–1} s^{–1}$. What is the reaction rate and rate of usage of reactant C?

Relevant Equations

kinetics equations

Hi,

I was attempting the following question and don't know how to find the 'reaction rate':
"For the reaction the following stoichiometric coefficients have been determined: 2 $C$ react to form 2 $E$ and 1 $F$. The rate of formation of E is $1.6\times10^{–4} mol L^{–1} s^{–1}$. What is the reaction rate and rate of usage of reactant C? "

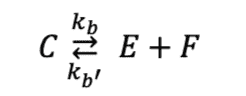
(note this form of the equation doesn't have the coefficients in front of it)

Attempt:
We can write the equations for the formation of E and C as follows:
$$\frac{de}{dt} = k_b c^2 - k_{b'} e^2 f = 1.6\times10^{–4} mol L^{–1} s^{–1}$$
$$\frac{dc}{dt} = k_{b'} e^2 f - k_b c^2$$
The second expression is just -1 times the first expression and I am assuming the: rate of formation = -1 * rate of usage. That all leads to the rate of usage of reactant C is $1.6 \times10^{–4} mol L^{–1} s^{–1}$.

Now I am confused on how to find the reaction rate. The answer says it should be $0.8\times10^{–4} mol L^{–1} s^{–1}$ which I can see is a factor of 2 (or 0.5) away from our current rate, but I don't know how to connect the two. A search on google shows that:
$$\text{reaction rate} = \frac{-\Delta \text{[reactants]}}{\Delta t}$$
but it isn't clear how I use that expression to get the required answer.

Thanks for any help

 

[etotheipi]

If the stoichiometric coefficient of a certain species $X_{\alpha}$ is $\nu_{\alpha}$ then the rate of reaction is defined to be$$r = \frac{1}{\nu_{\alpha}} \frac{d[X_{\alpha}]}{dt}$$[Note that here the stoichiometric coefficients are defined such that $\nu_{\alpha} < 0$ if $X_{\alpha}$ is a reactant; some texts instead define all of the $\nu_{\alpha}$ to be strictly positive and insert the signs in equations involving them by hand]

 

[Master1022]

Many thanks - that indeed leads to the 0.8! Hadn't seen that before.

If the stoichiometric coefficient of a certain species $X_{\alpha}$ is $\nu_{\alpha}$ then the rate of reaction is defined to be$$r = \frac{1}{\nu_{\alpha}} \frac{d[X_{\alpha}]}{dt}$$[Note that here the stoichiometric coefficients are defined such that $\nu_{\alpha} < 0$ if $X_{\alpha}$ is a reactant; some texts instead define all of the $\nu_{\alpha}$ to be strictly positive and insert the signs in equations involving them by hand]

 

[etotheipi]

No problem! The rate of change of concentration of a particular species is only scaled by its stoichiometric coefficient so that no matter which particular species you choose to measure, you always end up with the same value of $r$.