How Do Techni-Baryons Transform in SU(N_{TF}) and SU(2)_{spin} Symmetries?

[Andrea M.]

Consider a model with an exact $SU(N_{TC})$ techni-color symmetry and a $SU(N_{TF})_L\otimes SU(N_{TF})_R$ global techni-flavour symmetry which is spontaneously broken to the diagonal sub-group $SU(N_{TF})$ by condensates producing techni-pions (TC\pi) and techni-baryons(TCb).
What I'm trying to understand is how the various TCb transform under $SU(N_{TF})$ and $SU(2)_{spin}$.
Because the wave-function is totally antisymmetric in techni-color we expect that TCb must be fully symmetric in spin and techni-flavour. Following the line of thought of Georgi's chapter 15 I have embedded $SU(N_{TF})$ and $SU(2)_{spin}$ in a $SU(2N_{TF})$. The TCb transform under this $SU(2N_{TF})$ like a $N_{TC}$ completely symmetric combination, or in Young tableaux notation like a tableaux with $N_{TC}$ horizontal box. Now Georgi says that to understand what representation of $SU(N_{TF})$ and $SU(2)_{spin}$ are contained in the fully symmetric representation of $SU(2N_{TF})$ we must take the tensor product of all tableaux with $N_{TC}$ boxes of $SU(N_{TF})$ and $SU(2)_{spin}$ and see if they contain the fully symmetric representation. The results (see for example Chivukula, R.S. & Walker, T.P., 1989. Technicolor cosmology, Boston, MA: Boston Univ.) should be the following:
-For $N_{TC}=3$

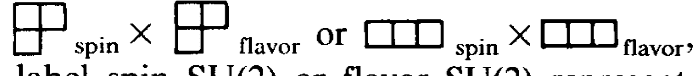
-For $N_{TC}=4$

The problem is that, except for the $N=3$ case, I'm not able to obtain the fully symmetric representation by taking the tensor product of this tableaux.

 

[fzero]

I don't think we necessarily need to have the totally symmetric representation of $SU(2N_{TF})$, just a representation that reduces to the trivial representation of $S_{N_{TC}}$. Any diagram that is trivial after deleting all rows with $N_{TC}$ or more boxes from the diagram will work. The totally symmetric representation for $SU(2N_{TF}$ will work, but so will others.

Looking at the products of the representations in your reference, we have

where in the middle line we actually have a few copies of the trivial $S_4$ representation appearing. For the missing representations like

we can see that we don't have enough boxes in the rows to make a trivial $S_4$ representation.

 

[Andrea M.]

I don't think we necessarily need to have the totally symmetric representation of SU(2NTF)SU(2N_{TF}), just a representation that reduces to the trivial representation of SNTCS_{N_{TC}}.

Yes I agree with this.

Any diagram that is trivial after deleting all rows with NTCN_{TC} or more boxes from the diagram will work. The totally symmetric representation for SU(2NTFSU(2N_{TF} will work, but so will others

Why I can delete all the rows with $N_{TC}$ or more boxes?
Am I wrong or the trivial representation of $S_4$ is a Young tableaux with 4 horizontal boxes?

 

[fzero]

Yes I agree with this.

Why I can delete all the rows with $N_{TC}$ or more boxes?
Am I wrong or the trivial representation of $S_4$ is a Young tableaux with 4 horizontal boxes?

Yes it is, but a Young tableaux with 4 horizontal columns of any equal size is also the trivial representation. So I mean delete in the same way that you would if you had a column with $N$ boxes for $SU(N)$.

 

[Andrea M.]

Could you suggest some reference where this result is derived?

 

[fzero]

Could you suggest some reference where this result is derived?

Georgi discusses the Young tableaux for $S_n$ in sects 1.21-24. The trouble is that we already know that irreps of $S_4$ never have more than 4 boxes so not all of the rules there apply (for instance we can't naively compute the dimension using 8 as the number of boxes). But we can assign $j$-cycles to the the boxes, so we get 4 2-cycles on 4 objects, which should be easy to show is reducible to 4 1-cycles.

 

[Andrea M.]

But we can assign jj-cycles to the the boxes, so we get 4 2-cycles on 4 objects, which should be easy to show is reducible to 4 1-cycles.

Are you sure? For example the four 2-cycles (12)(23)(14)(23) do not seem to be equivalent to four 1-cycles.

 

[fzero]

Are you sure? For example the four 2-cycles (12)(23)(14)(23) do not seem to be equivalent to four 1-cycles.

The rules of the Young Tableau are that the columns are the $j$-cycles and that we can't repeat an index in the same row. If we had a valid diagram, we would never repeat an index in any box, but with more than $n$ boxes we have to relax something.

With the above rules we only get elements like (13)(21)(34)(42) that are always reducible.