How do these LED lights conduct ?

[sherrellbc]

How do these LEDs conduct ?

With this board:

the associated schematic is:

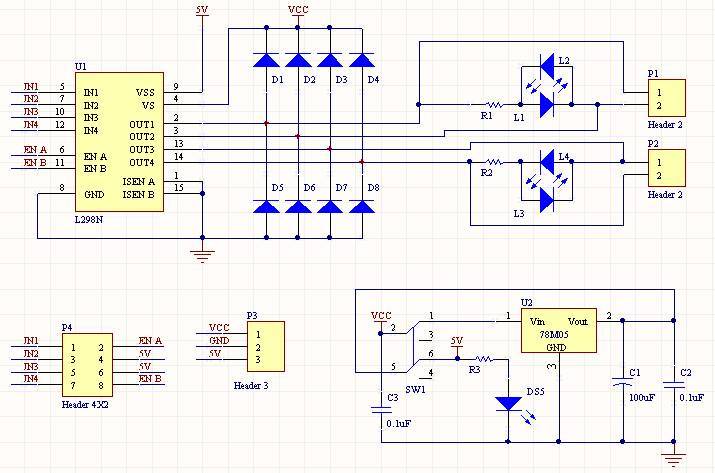
P1 (with pins 1 and 2) represents a motor. OUT1 and OUT2 are the conduction paths. LEDs L2 and L1 will illuminate depending on which way the H-Bridge is conducting.

My question is how are is that the LEDs conduct at all? It seems that the voltage across the resistor and LED is a function of the voltage across the motor. However, I thought that the voltage across a coil is essentially negligible given the constant current through it. However, are the LEDs drive by the fact that DC motors have inherent internal wire resistance? By my calculations, shown in my other thread regarding the L298 on this forum, I figured that my 3V motor had a 8 ohm internal resistance which demanded a 2.5V drop at 3mA current draw.

So that allowed 2.5V to exist across the LED and the associated current to be drawn through it?

Correct me if I am wrong on anything stated above.

 

[Baluncore]

A DC motor when stalled will have a current flow determined by it's winding resistance, the full supply voltage will still appear across the motor.

When a DC motor is running it will generate a back EMF, Vb, that is directly proportional to it's speed. That back EMF must be subtracted from the supply voltage, Vs, to get the voltage that appears across the internal winding resistance, Rs.

Ohm's law will then give you the current. I = (Vs – Vb) / Rs
The torque on a DC motor is directly proportional to that current flowing.

A DC motor should never short circuit it's supply.

When running without load it will have bearing friction, air drag and electrical resistance losses. The current needed when running without load is proportional to the combined torque of the friction and drag losses.

 

[sherrellbc]

Assuming we are talking about a basic configuration like this:

A DC motor when stalled will have a current flow determined by it's winding resistance, the full supply voltage will still appear across the motor.

Voltage across a coil is: L*di/dt

It seems that, even when turning, the current is constant and the voltage would be zero across the coil. Consequentially, the entire voltage that exists across the motor would be a proportional to the winding resistance and current through the motor. This should always be the case, right? Regardless of whether the motor is in a stalled state or not. Just checking my understanding.
--To go a bit further, with ideal wire, would it be that a motor would actually short the terminals of the supply when in steady-state? I know that the coil will, momentarily, oppose the current so there would be an impedance briefly.

When a DC motor is running it will generate a back EMF, Vb, that is directly proportional to it's speed. That back EMF must be subtracted from the supply voltage, Vs, to get the voltage that appears across the internal winding resistance, Rs.

Ohm's law will then give you the current. I = (Vs – Vb) / Rs
The torque on a DC motor is directly proportional to that current flowing.
.

I thought the back EMF was only generated a consequence of cutting the motor's conduction path (i.e. turning it "off" instantly). Following that event, the coil would generate an EMF such that the current that was originally flowing through the coil remained until the magnetic field energy was dissipated through resistance losses via heat.

Further, this is precisely the reason behind including flyback diodes, or similar, protection circuits.

A DC motor should never short circuit it's supply.

Is this a statement or a warning? Are you saying that, given the internal resistance, a motor will never short the supply terminals?

Or are you saying that you should never wire a motor such that it's connected to the positive and negative of the supply?

When running without load it will have bearing friction, air drag and electrical resistance losses. The current needed when running without load is proportional to the combined torque of the friction and drag losses.

It makes sense that the current through a motor without load is proportional to that (current) which is required to overcome the external forces on the motor. However, I am confused on your statement about the current through a motor without load being proportional to the torque of friction and drag losses.

It seems that it makes sense this would be the absolute minimum current required to turn the motor at all, but not necessarily the no-load operating current. That is, the current required to overcome the external torque (friction) forces exerted in the opposite direction of operation may be X amp (which may turn the motor ever so slightly continuously). However, the current to spin the motor very very fast (~10k rpm) would be some (X + Y) amps.

 

[Baluncore]

Voltage across a coil is: L*di/dt

No. That is the voltage across a perfect inductor. A DC motor comprises a series resistance plus an inductance. The inductance plays no part when the current is stable. You appear unwilling to accept that DC is not AC.

with ideal wire, would it be that a motor would actually short the terminals of the supply when in steady-state?

No. Only when it is stopped, but it would then develop a very high current = very high torque, so it will start and then the back EMF will cancel part of the supply. That contradicts the steady state you hypothesised. You need to stop making irrelevant idealistic assumptions that contradict reality. They are destructive and a waste of your time.

I thought the back EMF was only generated a consequence of cutting the motor's conduction path

You are wrong. Back EMF of a DC motor is proportional to RPM. It is the motor acting as a generator. It is inside the motor and must be subtracted from the supply voltage. Suddenly switching off the current through an inductor will also generate a back EMF.

Or are you saying that you should never wire a motor such that it's connected to the positive and negative of the supply?

That would be really stupid. You could not possibly use a motor if you did not connect it across the supply.

However, I am confused on your statement about the current through a motor without load being proportional to the torque of friction and drag losses .

Torque is directly proportional to current. When the only load is friction and drag losses, then that must determine the current.

That is, the current required to overcome the external torque (friction) forces exerted in the opposite direction of operation may be X amp (which may turn the motor ever so slightly continuously). However, the current to spin the motor very very fast (~10k rpm) would be some (X + Y) amps.

That is only true if there is a shaft torque due to your undefined current component Y.

You have completely ignored the key equation I = (Vs – Vb) / Rs
I detect an arrogance in your approach. Only when you are prepared to read and think in a non-hostile way will you begin to understand.

 

[sherrellbc]

No. That is the voltage across a perfect inductor. A DC motor comprises a series resistance plus an inductance. The inductance plays no part when the current is stable. You appear unwilling to accept that DC is not AC.

What? That equation must be used in conjunction with the internal resistance of the winding. I was speaking only of the inductance at this point but later elaborate with respect to the series resistance. The equation is wholly valid regardless of a DC or AC application. In DC, the current differential is zero and no voltage exists across the coil.

All you did was restate exactly what my question was and make a judgement of my will. Your statements are not making sense. You say that I am wrong, then state that in a coil, with constant current, "takes no part." This is exactly what I said would happen and the subject of my question to you for verification.

No. Only when it is stopped, but it would then develop a very high current = very high torque, so it will start and then the back EMF will cancel part of the supply. That contradicts the steady state you hypothesised. You need to stop making irrelevant idealistic assumptions that contradict reality. They are destructive and a waste of your time.

These irrelevant idealistic concepts are the basis for what really happens. It may be your opinion that such things are irrelevant, but I believe they are vital to full comprehension of any problem. Understanding the base case further facilitates understanding the more complicated ones.

You are wrong. Back EMF of a DC motor is proportional to RPM. It is the motor acting as a generator. It is inside the motor and must be subtracted from the supply voltage. Suddenly switching off the current through an inductor will also generate a back EMF.

I am right, but have not considered the other times EMF is generated. You state below that I exhibit arrogance, yet you reply in this manner here and above.

That would be really stupid. You could not possibly use a motor if you did not connect it across the supply.

You are making a literal assumption here and not fully considering what I wrote. By not applying the motor across the supply I meant perhaps having a series resistance as well or something to protect a short circuit of the supply's terminals (if that could happen - which is another question I had asked).

Torque is directly proportional to current. When the only load is friction and drag losses, then that must determine the current.

I understand this concept but further elaborated my confusion with the following sentence with an attempt at an example.

That is only true if there is a shaft torque due to your undefined current component Y.

What I was trying to illustrate here was if, for example, 100mA is the absolute minimum current required to drive the motor at its absolute slowest possible rate (perhaps this results in about 1rpm or so) then that appears to be the current required to overcome the frictional and drag forces. So, with that, the X amps I wrote earlier would be the 1mA minimum current.

My confusion was that you had said the no-load current would be equal to the current that was required to overcome these forces. However, the motor - when ran at no load - may be ~10k rpms and drawing a current substantially higher than the minimum current required to move it very slowly (this slow-turning current drawn is the current required to overcome those external forces). This extra current I wrote as being Y Amps. So, in this way, the no-load operating current would be (X+Y) Amps.

But it was confusing to me because this operating current is much greater than the current required to overcome the external forces. You can drive half that current with a reduced speed.

You have completely ignored the key equation I = (Vs – Vb) / Rs
I detect an arrogance in your approach. Only when you are prepared to read and think in a non-hostile way will you begin to understand.

I am completely open to new concepts and corrections of my misconceptions. I have not been hostile in any way. Maybe it's that I first say "I thought .." before addressing your comments that you think this. I do that because I hope to portray my understanding in hopes of a full correction in all areas of where I have gone astray.

I cannot accept the equation until I understand where it derives from. That is why I asked questions per statement you made.

Your comments are the ones in which a subtle notion of arrogance is present.
I am doing nothing more than stating what it is that I currently have as my understanding and then ask questions to remedy my misconceptions.

This has really snow-balled into something much larger with lots of things I am not fully certain about, but I still do not understand how those LED I mentioned in the OP operate. Is it that the design exploits the fact that the motor will have at least ~1.5V or so across its leads there forward-biasing the diodes?

After all of the preceding posts it seems this is the case.

It seems that the LEDs would not conduct if the motor is a low-voltage variety unless the diodes have very low Vf.

 

[Baluncore]

See http://mplab.ucsd.edu/tutorials/DC.pdf

 

[sherrellbc]

See http://mplab.ucsd.edu/tutorials/DC.pdf

Thank you, I have actually been looking for something like this.