How do vectors play a role in ship navigation?

[mathmari]

Hey!

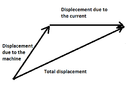
We suppose that a ship, that is at the position $(1, 0)$ of a nautical map (with the North at the positive direction $y$) and it "sees" a rock at the position $(2, 4)$, is directed to North and is traveling $4$ knots in the relation to the water.
There is a current of 1 knot that is directed to the east side.
The units on the map are nautical miles, $1$ knot=$1$ nautical mile per hour.

a) If there weren't the current, which vector $\overrightarrow{u}$ would represent the velocity of the ship in relation to the see floor?

b) If the ship was just following the current, which vector $\overrightarrow{v}$ would represent the velocity in relation to the see floor?

c) Which vector $\overrightarrow{w}$ represents the total velocity of the ship?

d) Where will the ship be after $1$ hour?

e) Does the captain have to change direction?

f) What would happen if the rock was an iceberg?
Could you give me some hints how I could do this exercise?? (Wondering)

What does it mean "...which vector would represent the velocity of the ship in relation to the see floor?" ?? (Wondering)

 

[Evgeny.Makarov]

a) If there weren't the current, which vector $\overrightarrow{u}$ would represent the velocity of the ship in relation to the see floor?

b) If the ship was just following the current, which vector $\overrightarrow{v}$ would represent the velocity in relation to the see floor?

Surely you should be able to sea it. (Smile)

c) Which vector $\overrightarrow{w}$ represents the total velocity of the ship?

$w=u+v$.

d) Where will the ship be after $1$ hour?

$(1,0)+w$.

f) What would happen if the rock was an iceberg?

Then it would be carried by the current.

What does it mean "...which vector would represent the velocity of the ship in relation to the see floor?" ?

Let $A$ be the projection of the ship onto the sea floor. Let $B$ the projection of the ship onto the sea floor one hour later. Then "the vector that represents the velocity of the ship in relation to the sea floor" is $\overrightarrow{AB}$.

 

[mathmari]

Surely you should be able to sea it. (Smile)

(Blush)

$w=u+v$.

$(1,0)+w$.

Then it would be carried by the current.

Could you explain to me why these are the answers? I haven't understood it.

Let $A$ be the projection of the ship onto the sea floor. Let $B$ the projection of the ship onto the sea floor one hour later. Then "the vector that represents the velocity of the ship in relation to the sea floor" is $\overrightarrow{AB}$.

Why do we have to find the projection of the ship onto the sea floor one hour later?

 

[Evgeny.Makarov]

Why do we have to find the projection of the ship onto the sea floor one hour later?

My guess is that you are trying to solve problems about velocity without understanding what velocity is. Please note that constant and average velocities (as opposed to instantaneous velocity, which relies on the concept of a derivative) are middle or high school topics.

 

[mathmari]

In my book there is the following:

If a body moves with uniform velocity on a line, then the velocity vector is a displacement vector from its position at a moment till the position $1$ unit time later. Does uniform velocity means constant velocity?

a) The ship is traveling to North 4 knots and there is no current. That means that we have the following:

View attachment 4037

So $\overrightarrow{u}=(1, 4)$.

Is it correct?

b) The ship follows the current.

In my book at an other example there is the following:

View attachment 4033

Could you explain to me why it is like that?

c) Why is the total velocity of the ship $\overrightarrow{w}=\overrightarrow{u}+\overrightarrow{v}$ ?

d) The position of the ship in $1$ hour is "$\text{ Initial position + Total velocity} =(1, 0)+\overrightarrow{w}$, right?

e) After $1$ hour the ship will be at the position $(4, 8)$ which is the same line as the position of the rock $(2, 4)$. So, the captain has to change direction.

f) "Then it would be carried by the current."

Could you explain it further to me?