- #1
Waqas Asad
- 1
- 0
I want to know that how we create a graph by using the following parameters,,,,,
i.e x, n and m.
For example in the figure a curve for Jo(x) is starting from the point 1 on Y-axis and then crossing at point 2.2 on X-axis. In this case n=o but what are the value of x and m for the curve Jo(x)?
Remember the graph is for First Kind of Bessel Function...
Here is the picture of that graph...
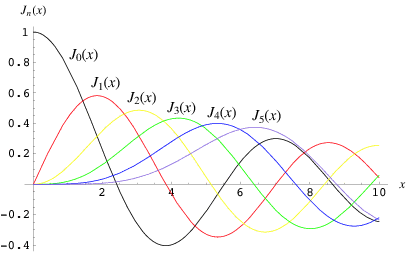
Waiting for a perfect answer.
i.e x, n and m.
For example in the figure a curve for Jo(x) is starting from the point 1 on Y-axis and then crossing at point 2.2 on X-axis. In this case n=o but what are the value of x and m for the curve Jo(x)?
Remember the graph is for First Kind of Bessel Function...
Here is the picture of that graph...
Waiting for a perfect answer.