How do we distribute the elements into schedules?

  • MHB
  • Thread starter mathmari
  • Start date
  • Tags
    Elements
In summary: E))\end{align*} So $S_2$ is conflict serializable. Then we have to swap $(T_5,R, C), (T_6,R, D)$, since they are both R and they refer to the same object C. \begin{align*} &((T_1,R, A),(T_1,W, A), (T_2,R, A),(T_1,W, A), \\ &(T_1,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C
  • #1
mathmari
Gold Member
MHB
5,049
7
Hey! :giggle:

The transactions $T_1, T_2,\ldots , T_7$, the database elements $A, B, C, D, E$ and the below multiset are given
1639981654573.png


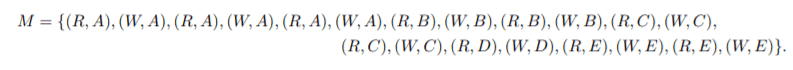
Now distribute the twenty elements from $M$ in three different ways so that three different schedules $S_1$, $S_2$ and $S_3$ arise. Also make sure that $S_1$ is a serial schedule, $S_2$ is a conflict serializable schedule, and $S_3$ is a non-conflict serializable schedule. Give the dependency graphs on S2 and S3.Do we distribute the elements of $M$ to the transactions $T_i$ arbitrarily ? :unsure:
 
Last edited by a moderator:
Physics news on Phys.org
  • #2
Can we first define arbitrarily the seven transactions and then define the three schedules so that $S_1$ is a serial schedult, $S_2$ is conflict serializableand $S_3$ is non-conflict serializable?

We have twenty elements and seven transactions, so should each transaction contain two elements and the six of the transactions have also a third element?

Do we define the transaction for example as follows ?
\begin{align*}&T_1 : ((R, A),(W, A)) \\ &T_2: ((R, A),(W, A)(R, A)) \\ &T_3 : ((W, A),(R, B),(W, B)) \\ &T_4 : ((R, B),(W, B),(R, C)) \\ &T_5: ((W, C), (R, C),(W, C)) \\ &T_6: ((R, D),(W, D),(R, E)) \\ &T_7 : ((W, E),(R, E),(W, E))\end{align*}
Is then a serial schedule \begin{align*}S_1&=((T_1, R, A),(T_1, W, A),(T_2, R, A),(T_2, W, A),(T_2, R, A),\\ & (T_3, W, A),(T_3, R, B),(T_3, W, B),(T_4, R, B),(T_4, W, B),(T_4, R, C),\\ & (T_5, W, C), (T_5, R, C),(T_5, W, C),(T_6, R, D),(T_6, W, D),(T_6, R, E),\\ & (T_7, W, E),(T_7, R, E),(T_7, W, E))\end{align*} ?

:unsure:
 
  • #3
Hey mathmari!

After reading you notes in your other thread, I believe you are correct. (Nod)
 
  • #4
Klaas van Aarsen said:
After reading you notes in your other thread, I believe you are correct. (Nod)

A schedule is called conflict serializable if it can be transformed into a serial schedule by swapping non-conflicting operations.

So we take $S_1$ and we swap at least two non-conflicting operations to get $S_2$. Is that correct?

So do we get the following ?
\begin{align*}S_2&=((T_7, W, E),(T_1, W, A),(T_2, R, A),(T_2, W, A),(T_2, R, A),\\ & (T_3, W, A),(T_3, R, B),(T_3, W, B),(T_4, R, B),(T_4, W, B),(T_4, R, C),\\ & (T_5, W, C), (T_5, R, C),(T_5, W, C),(T_6, R, D),(T_6, W, D),(T_6, R, E),\\ & (T_1, R, A) ,(T_7, R, E),(T_7, W, E))\end{align*} (I swapped the first element of the first line with the first element of the last line) Is that a conflict serializable schedule ? The result is not unique, is it? :unsure: For $S_3$ we have to consider a schedule at which even when we swap non-conflicting operations we don't get a serial schedule, right? :unsure:
 
  • #5
I'm afraid that is not correct. (Shake)

In transaction $T_1$ we first read from A, and then we write to A.
When we put that read operation near the end, we will read what we (or some other transaction) wrote before, instead of what was there before we wrote.
In other words, the conflicting operations in the same transaction must remain in the same order. 🤔

I believe that we can also not put $(T_7, W, E)$ at the beginning, since then $T_7$ is not atomic any more. Other transactions will read the changed value in E while transaction $T_7$ has not been completed yet, and it will still read and write yet again to E. 🤔

Other than that, yes, we can just swap 2 operations, as long as we make sure that the transactions remain atomic and consistent. 🤔
 
  • #6
Klaas van Aarsen said:
In transaction $T_1$ we first read from A, and then we write to A.
When we put that read operation near the end, we will read what we (or some other transaction) wrote before, instead of what was there before we wrote.
In other words, the conflicting operations in the same transaction must remain in the same order. 🤔

So when we move $(T_1, R,A)$ do we have to move also $(T_1, W, A)$ so that is again after $(T_1, R, A)$ ? :unsure:
Klaas van Aarsen said:
I believe that we can also not put $(T_7, W, E)$ at the beginning, since then $T_7$ is not atomic any more. Other transactions will read the changed value in E while transaction $T_7$ has not been completed yet, and it will still read and write yet again to E. 🤔

What do you mean by atomic? I got stuck right now. :unsure:
 
  • #7
If we just swap $(T_5, W, C)$ and $(T_6, R, D)$, do we get a conflict serializable schedule or do we have to do more swaps ? \begin{align*}&((T_1, R, A),(T_1, W, A),(T_2, R, A),(T_2, W, A),(T_2, R, A),\\ & (T_3, W, A),(T_3, R, B),(T_3, W, B),(T_4, R, B),(T_4, W, B),(T_4, R, C),\\ & (T_5, W, C), (T_5, R, C),\textbf{(T_6, R, D)},\textbf{(T_5, W, C)},(T_6, R, D),(T_6, W, D),(T_6, R, E),\\ & (T_7, W, E),(T_7, R, E),(T_7, W, E))\end{align*}
:unsure:
 
  • #8
In general the transactions should always be in the form R-W or R-W-R-W ?

Then should the transactions be as follows ?
\begin{align*}&T_1 : ((R, A),(W, A), (R, A),(W, A)) \\ &T_2: ((R, A),(W, A)) \\ &T_3 : ((R, B),(W, B),(R, B),(W, B)) \\ &T_4 : ((R, C),(W, C)) \\ &T_5: ( (R, C),(W, C)) \\ &T_6: ((R, D),(W, D)) \\ &T_7 : ((R, E),(W, E),(R, E),(W, E))\end{align*}

:unsure:
 
  • #9
Then we have :
\begin{align*}S_1 : &((T_1,R, A),(T_1,W, A), (T_1,R, A),(T_1,W, A), \\ &(T_2,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_5,W, C), (T_6,R, D),(T_6,W, D), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*} We can swap $(T_5,W, C), (T_6,W, D)$ since they have different objects, so they are not in conflict.
\begin{align*} &((T_1,R, A),(T_1,W, A), (T_1,R, A),(T_1,W, A), \\ &(T_2,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_6,W, D), (T_6,R, D),(T_5,W, C), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*}
We can also swap $(T_1,R, A), (T_2,R, A)$ since they are both R, so they are not in conflict.
So we get:
\begin{align*}S_2 : &((T_1,R, A),(T_1,W, A), (T_2,R, A),(T_1,W, A), \\ &(T_1,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_6,W, D), (T_6,R, D),(T_5,W, C), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*} We can swap $(T_1,R, A),(T_1,W, A)$ since they are in conflict
\begin{align*} &((T_1,R, A),(T_1,W, A),(T_1,W, A), (T_1,R, A), \\ &(T_2,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_5,W, C), (T_6,R, D),(T_6,W, D), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*}
We can swap also $(T_1,R, A),(T_2,W, A)$ since they are in conflict
\begin{align*}S_3 : &((T_1,R, A),(T_1,W, A),(T_1,W, A), (T_2,W, A), \\ &(T_2,R, A),(T_1,R, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_5,W, C), (T_6,R, D),(T_6,W, D), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*} Are these schedules correct? :unsure:
 

FAQ: How do we distribute the elements into schedules?

How are elements prioritized when creating schedules?

The prioritization of elements in a schedule depends on the specific goals and objectives of the schedule. Some elements may be more important than others, and therefore, will be given higher priority. This could be based on factors such as deadlines, resources, or importance to the overall project.

What factors are considered when determining the distribution of elements in a schedule?

There are several factors that are typically considered when determining the distribution of elements in a schedule. These may include the availability of resources, the complexity and duration of each element, dependencies between elements, and any external factors that may affect the schedule.

How do we ensure that the distribution of elements in a schedule is efficient?

To ensure efficiency in the distribution of elements in a schedule, it is important to carefully analyze and plan the schedule. This may involve breaking down larger elements into smaller, more manageable tasks, identifying and resolving any potential conflicts or dependencies, and regularly reviewing and adjusting the schedule as needed.

How do we handle changes or delays in the distribution of elements in a schedule?

Changes or delays in the distribution of elements in a schedule are common and can be handled by regularly reviewing and updating the schedule. This may involve re-prioritizing elements, adjusting timelines, and communicating any changes to team members or stakeholders. It is important to be flexible and adaptable when managing changes in a schedule.

What tools or methods are commonly used to distribute elements into schedules?

There are various tools and methods that can be used to distribute elements into schedules. These may include project management software, Gantt charts, Kanban boards, and other visual planning tools. It is also common to use techniques such as timeboxing or Agile methodologies to efficiently distribute and manage elements in a schedule.

Similar threads

MHB Transactions & schedules - Dependency relations
Replies
1
Views
748
I Enumerating a Large Ordinal: Can We Find a Limit to the Continuum?
Replies
27
Views
3K

Hot Threads

Recent Insights

Back
Top