How do we find the dimensions of a rectangle given its perimeter and diagonal?

[Simonio]

Hi, I can do basic quadratics but don't know how to apply them to the following problems:

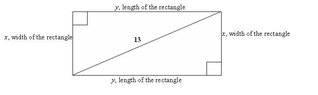
The perimeter of a rectangle is 34cm. Given that the diagonal is of length 13cm and the width is \(x \)cm, derive the equation \(x^2-17x+60=0\). hence find the dimensions of the rectangle.

(My first go at using Latex-hope it works!). Not sure how to apply the information about the diagonal and derive equation -if anyone can get me started , I'd be really grateful. Thanks.

 

[anemone]

Hi Simonio,

Your $\LaTeX$ works fine, well done!(Clapping)

For your problem, I think it'd be useful to first draw a rectangle and label using variables like $x$ and $y$ to represent its width and length, like what I did as follows:

View attachment 2581
Remember we're given that the perimeter of the rectangle is 34 cm, now, how to add up the perimeter of the rectangle above that its length and width are represented by the variables $y$ and $x$? Surely it is $2x+2y=34$, right? This equation can be simplified by dividing through the both sides of the equation by 2, thus we have

$2x+2y=34$

$x+y=17$(*)

Next, notice that we can form right triangle from the rectangle above and it follows from the Pythagoras theorem that $13^2=x^2+y^2$(**).

Up to this point, we have a total of two equations in terms of two variables, $x$ and $y$ but what we're required to prove is the quadratic equation $x^2-17x+60=0$.

We know there is no $y$ in that equation. So, we need to get rid of $y$ but how? The easiest way is to rewrite the equation (*) as the subject of $y$ and then replace it in the equation (**):

From $x+y=17$(*), we get $ y=17-x$

Replace this $y=17-x$ in the equation (**) we have

$13^2=x^2+(17-x)^2$

Now, can you proceed? We can finish it even without the help of a calculator to find for the values of both $13^2$ and $17^2$!

 

[Simonio]

Thank you very much Anemone -that's a great help. I thought I needed to use the Pythagoras theorem but wasn't sure. brilliant help! many thanks!

 

[Simonio]

Hi Anemone,

Having looked at it I'm still not sure hoe to proceed with the \(17^2\) and the \(13^2\)-how do you get rid of the indices? Thanks.

 

[anemone]

Hi Anemone,

Having looked at it I'm still not sure hoe to proceed with the \(17^2\) and the \(13^2\)-how do you get rid of the indices? Thanks.

Hmm...I'm less sure if you're familiar with the different of two squares or not...so, if you're not, then please proceed with using a calculator to help you out with the addition. But if you're familiar with it, recall that the difference of two squares is a squared number subtracted from another squared number, and they can be factored according to the identity $x^2-y^2=(x+y)(x-y)$.

We'll see how this is going to help us in this problem:

We know we have $13^2=x^2+(17-x)^2$, we expand the RHS, and collect like terms and then move all terms to either side, we get

$13^2=x^2+17^2-34x+x^2$

$0=2x^2-34x+17^2-13^2$

$2x^2-34x+17^2-13^2=0$

Notice that $17^2-13^2$ is the difference of two squares and they can be simplified fairly easily because they can be represented by other form, which is $17^2-13^2=(17+13)(17-13)$. So,

$2x^2-34x+17^2-13^2=0$ becomes

$2x^2-34x+(17+13)(17-13)=0$

$2x^2-34x+(30)(4)=0$

Divide through the equation by 2 we ended up with

$x^2-17x+(30)(2)=0$ or

$x^2-17x+60=0$ and we're done!(Sun)