How Do You Calculate Angular Acceleration from Tangential Acceleration?

[makeAwish]

Disk rotating problem. urgent, help pls..

Homework Statement

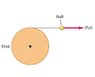
A disk of radius 30.0cm is free to turn about an axle perpendicular to it through its center. It has very thin but strong string wrapped around its rim, and the string is attached to a ball that is pulled tangentially away from the rim of the disk. The pull increases in magnitude and produces an acceleration of the ball that obeys the equation a(t) = At , where t is in seconds and A is a constant. The cylinder starts from rest, and at the end of the third second, the ball's acceleration is 1.50 m/s^2.

a. Express the angular acceleration of the disk as a function of time.

b. How much time after the disk has begun to turn does it reach an angular speed of 17.5 rad/s?
c. Through what angle has the disk turned just as it reaches 17.5 rad/s?

The attempt at a solution


I have found A to be 0.500m/s^3.

but i duno how to do part a.


can help me pls?
thanks!

 

[makeAwish]

i tried applying angular acceleration, alpha = r/a where a is tangential acceleration. and i get 0.3/(0.5t)

the answer shld be in (rad/s^3)t units. and is independent on t..

 

[tiny-tim]

Hi janettaywx!

(have an alpha: α )

A disk of radius 30.0cm is free to turn about an axle perpendicular to it through its center. It has very thin but strong string wrapped around its rim, and the string is attached to a ball that is pulled tangentially away from the rim of the disk. The pull increases in magnitude and produces an acceleration of the ball that obeys the equation a(t) = At , where t is in seconds and A is a constant. The cylinder starts from rest, and at the end of the third second, the ball's acceleration is 1.50 m/s^2.

a. Express the angular acceleration of the disk as a function of time.
…
I have found A to be 0.500m/s^3.

No, A = 0.500m/s

i tried applying angular acceleration, alpha = r/a where a is tangential acceleration. and i get 0.3/(0.5t)

the answer shld be in (rad/s^3)t units. and is independent on t..

No, look at the dimensions …

angular acceleration (α) is in rad/s²,

and ordinary acceleration (a) is in m/s²,

and r is in m,

so a = rα, and α = a/r

 

[makeAwish]

hahah. thanks for the alpha.

hmm. but i tot A is accel divide by time.. so its units is rad/s³?

so α = 0.5t/0.3 ?

 

[makeAwish]

hmm.. it shld be indpt of t.. what shld i do next?

 

[tiny-tim]

hmm. but i tot A is accel divide by time.. so its units is rad/s³?

so α = 0.5t/0.3 ?

sorry, I misread it … you're right, it is m/s³

hmm.. it shld be indpt of t..

No, α = 0.5t/0.3 is ok … it should be a function of t

(because a = At, and α = a/r, so α = At/r )

 

[makeAwish]

hmm. say i want to convert it to radians, is this how we convert?

1rev -> 2∏ rad
1 rev = 2∏r = 2∏(0.3m)
so 2∏(0.3m) = 2∏ rad
0.3m -> 1 rad


and 1m -> (1/0.3)rad
den 0.5 m/s^3 = 0.5*(1/0.3) rad/s^3?

 

[makeAwish]

actually, from my qns here, they sae we shld get an answer indpt of t. but i don't rly noe why cos' it is a function of t...

 

[tiny-tim]

hmm. say i want to convert it to radians

(why ∏? everyone uses π )

No, it's already in radians …

the radian is defined specially so that α = a/r (or ω = v/r) works without adjustment.

 

[makeAwish]

i see. okay thanks!

 

[makeAwish]

but how u do 2nd part?? to find the time.

i tried taking time = angular speed / angular accel = 10.5s
but wrong..

 

[tiny-tim]

Hi janettaywx!

You have angular acceleration as a function of time …

inegrate it to get angular speed as a function of time

 

[makeAwish]

Hi janettaywx!

You have angular acceleration as a function of time …

inegrate it to get angular speed as a function of time

hi!

means i will get (1.67t^2) / 2 = 17.5
so t = 4.58s?

 

[makeAwish]

ok i got it. thanks a lot!

 

[tiny-tim]

means i will get (1.67t^2) / 2 = 17.5
so t = 4.58s?

Looks good