- #1
Chen
- 977
- 1
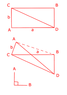
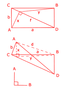
Ok, you take a rectangular and fold it along one of its diagonal, so that the two planes are perpendicular to each other.
Using [tex]a[/tex] and [tex]b[/tex], what is the distance between the points A and B ([tex]d[/tex])?
My anwer is:
[tex]d = \sqrt{a^2 + b^2 - \frac{2a^2b^2}{a^2 + b^2}} = \sqrt{\frac{a^4 + b^4}{a^2 + b^2}}[/tex]
But I doubt that it's actually correct. :)
Using [tex]a[/tex] and [tex]b[/tex], what is the distance between the points A and B ([tex]d[/tex])?
My anwer is:
[tex]d = \sqrt{a^2 + b^2 - \frac{2a^2b^2}{a^2 + b^2}} = \sqrt{\frac{a^4 + b^4}{a^2 + b^2}}[/tex]
But I doubt that it's actually correct. :)
Attachments
Last edited: