How Do You Calculate the Force on a Junction Point in a Two-Spring System?

[makeAwish]

Homework Statement

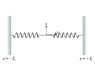
The ends of two identical springs are connected. Their unstretched lengths l are negligibly small and each has spring constant k. After being connected, both springs are stretched an amount L and their free ends are anchored at y=0 and x= (plus minus)L as shown (Intro 1 figure) . The point where the springs are connected to each other is now pulled to the position (x,y). Assume that (x,y) lies in the first quadrant.

a) What is the potential energy of the two-spring system after the point of connection has been moved to position (x,y)? Keep in mind that the unstretched length of each spring l is much less than L and can be ignored.
Express the potential in terms of k, x, y, and L.

b) Find the force F on the junction point, the point where the two springs are attached to each other.
Express F as a vector in terms of the unit vectors x and y.



The attempt at a solution

I can only solve part one.

For second part,

my force for the string on the left (lets say force1) = kx1(cos angle1)i + kx1(sin angle1)j and
my force for the string on the right (lets say force2) = kx2(cos angle2)i + kx2(sin angle2)j

then i sub in the cos angles and sin angles,

my total force is 2kLi + 2kyj

fyi: my i and j are the unit vectors.

but the answer is wrong. it is independent of L..


Can help me pls?? Thank you!

 

[Delphi51]

I agree with your force expressions with cos and sin except that the x component in force 1 should be negative. And both y components should be negative.
F = -2kLi - 2kyj
Note that the x component has an L in it, so it is not independent of L.

 

[nlightner]

Hi there,

I can see that you have attempted to solve the problem and have a good understanding of the concept. However, I believe you have made a small mistake in your calculation for the force on the junction point.

Since the two springs are identical and have the same spring constant k, the force exerted by each spring on the junction point would also be equal. So, the total force on the junction point would be the sum of these two forces.

Using your notation, the force on the junction point would be:

F = (kx1 cos(angle1) + kx2 cos(angle2))i + (kx1 sin(angle1) + kx2 sin(angle2))j

Now, to simplify this further, we know that x1 = x and x2 = y (since they are the coordinates of the junction point). Also, since the angle between the two springs is 90 degrees, cos(angle1) = sin(angle2) and sin(angle1) = cos(angle2). Substituting these values, we get:

F = (kx + ky)i + (kx + ky)j

= (kx + ky)(i + j)

= k(x + y)(i + j)

Therefore, the force on the junction point is dependent on both x and y, as well as the spring constant k. I hope this helps you understand the problem better. Keep up the good work!