- #1
toniojesusde
- 1
- 0
[Moderator note: This is an old thread from 2010. But it sounds like a good question, so I moved it here and bumped it to the top.]
Hello, this is my first post to PF. I've been trying to find out my answer in similar posts (resistance of a disk, ...) with no luck. So I would really appreciate some help. Here's the thing:
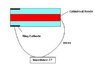
I am trying to calculate the impedance of an electrode submerged in sea water, using a ring shaped counter electrode (the attached images depicts the system).
In order to find out a value I decompose the cylinder in diferential surfaces dS, and calculate the resistance for each element using R_dS=R_sx/(2∙π∙r∙dx)
Where R_sx can be R_s1 (for those elements of the electrode that overlap with the cathode) or R_s2 (for the rest of the elements)
R_s1=ρ∙d, being ρ the resistivity of the electrolyte and d the distance between the cathode and the anode (electrode).
R_s2=ρ∙√(d^2+x^2 ), being x the distance in the x-axis between the right border of the cathode and the considered diferential element.
to calculate total resistance i do the inverse of the sum of the inverses of all the diferential resistances. (that a tongue twister! )
)
Is this whole solution valid? I assume that all the current lines of the elements separated from the cathode go from the electrode to the same point (right border) of the cathode, is that the real situation? any suggestions for improving the model? Thanks a lot guys, you are the best, keep up with the hard work.
Hello, this is my first post to PF. I've been trying to find out my answer in similar posts (resistance of a disk, ...) with no luck. So I would really appreciate some help. Here's the thing:
I am trying to calculate the impedance of an electrode submerged in sea water, using a ring shaped counter electrode (the attached images depicts the system).
In order to find out a value I decompose the cylinder in diferential surfaces dS, and calculate the resistance for each element using R_dS=R_sx/(2∙π∙r∙dx)
Where R_sx can be R_s1 (for those elements of the electrode that overlap with the cathode) or R_s2 (for the rest of the elements)
R_s1=ρ∙d, being ρ the resistivity of the electrolyte and d the distance between the cathode and the anode (electrode).
R_s2=ρ∙√(d^2+x^2 ), being x the distance in the x-axis between the right border of the cathode and the considered diferential element.
to calculate total resistance i do the inverse of the sum of the inverses of all the diferential resistances. (that a tongue twister!
Is this whole solution valid? I assume that all the current lines of the elements separated from the cathode go from the electrode to the same point (right border) of the cathode, is that the real situation? any suggestions for improving the model? Thanks a lot guys, you are the best, keep up with the hard work.
Attachments
Last edited by a moderator: