How Do You Calculate Values Using pV Diagrams for a Monatomic Gas?

  • #1
cheetah
2
0
Homework Statement
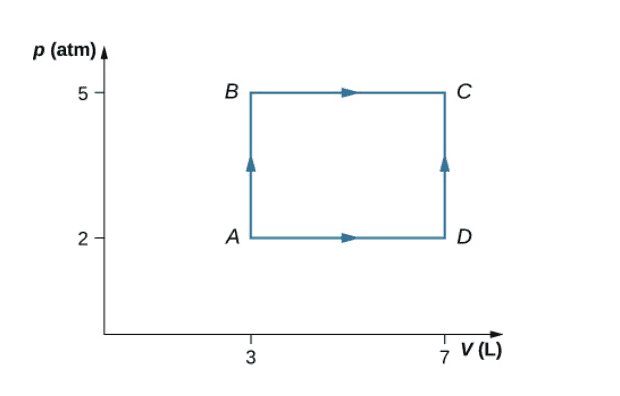
Consider the processes shown in Fig. 1 for a monatomic gas.
a) Find the work done in each of the processes AB, BC, AD, and DC.
b) Find the internal energy change in processes AB and BC.
c) Find the internal energy difference between states C and A.
d) Find the total heat added in the ADC process.
e) From the information given, can you find the heat added in process AD? Why or why
not?
Relevant Equations
Eint = Q − W
I’m having trouble with a Thermodynamics Assignment and could use some help. I’ve been given the below graph and told to consider the processes shown for a monatomic gas. I’ve been asked to answer these questions with no further information besides the graph.
1710793385005.png
 
Physics news on Phys.org
  • #2
Welcome to PF. :smile:

We are not allowed to help you until you show some effort on your problem. What parts can you start working on? It's hard to believe you have been given this question without the material having been covered in class or in your textbook.
 
  • #3
I believe I've solved question a.
AB and DC = 0 (since they're constants)
BC = 20 (2026J)
AD = 8 (810.4J)
 
  • #4
That's helpful. What equations did you use to calculate those values?
 

FAQ: How Do You Calculate Values Using pV Diagrams for a Monatomic Gas?

1. What is a pV diagram and how is it used for a monatomic gas?

A pV diagram, or pressure-volume diagram, is a graphical representation of the changes in pressure (p) and volume (V) of a gas. For a monatomic gas, such as helium or neon, this diagram helps visualize thermodynamic processes and can be used to calculate work done by or on the gas, as well as changes in internal energy and temperature.

2. How do you calculate work done by a monatomic gas using a pV diagram?

The work done by a monatomic gas during a thermodynamic process is represented by the area under the curve on a pV diagram. For an isobaric process (constant pressure), the work done is W = pΔV. For an isochoric process (constant volume), no work is done (W = 0). For an isothermal process (constant temperature), the work done is W = nRT ln(Vf/Vi), where n is the number of moles, R is the gas constant, and Vi and Vf are the initial and final volumes, respectively.

3. How do you determine changes in internal energy for a monatomic gas using a pV diagram?

For a monatomic ideal gas, the change in internal energy (ΔU) depends only on the change in temperature, not on the path taken. It can be calculated using ΔU = (3/2)nRΔT, where n is the number of moles, R is the gas constant, and ΔT is the change in temperature. From a pV diagram, if you can determine the initial and final states (p, V, T), you can calculate ΔT and thus ΔU.

4. How do you use a pV diagram to identify different thermodynamic processes for a monatomic gas?

Different thermodynamic processes can be identified on a pV diagram by the shape of the curve:- Isothermal process: A hyperbolic curve where temperature remains constant.- Isobaric process: A horizontal line where pressure remains constant.- Isochoric process: A vertical line where volume remains constant.- Adiabatic process: A steeper curve than the isothermal curve where no heat is exchanged.By identifying these curves, you can determine the type of process and apply the appropriate equations.

5. How do you calculate the heat added or removed from a monatomic gas using a pV diagram?

To calculate the heat added or removed (Q) from a monatomic gas, you can use the first law of thermodynamics: ΔU = Q - W, where ΔU is the change in internal energy and W is the work done by the gas. From a p

Similar threads

Finding Values Using Fe-C Diagram for Materials Engineering Assignment
Replies
3
Views
1K
Engineering Calculating the mass of air in a pressurised air tank
Replies
14
Views
2K
Engineering How do I draw the Bode diagram of this transfer function?
Replies
3
Views
2K
PV Diagram of Ideal Monatomic Gas Processes
Replies
4
Views
2K
Thermodynamics -- calculating fluid mass
Replies
7
Views
3K
Thermodynamics: using Peng-Robinson's equation of state
Replies
3
Views
2K
Isochoric Process with Unknown Ideal Gas
Replies
5
Views
2K
How to Plot a Thermodynamic Cycle in T-s Diagram?
Replies
2
Views
1K
Thermodynamics: Gas pressure and change in volume
Replies
6
Views
3K
Plotting Carnot Engine Cycle on PV Diagram
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top