How Do You Calculate Velocities Using the Cosine Formula?

[jkh4]

Given the following image and formula:

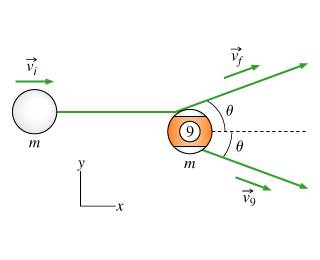
cos(x) = (vi)/(vf+V9)

how do you find the value for each of the velocity? I try using Pythagoras theory for the triangel but no use...

 

[HallsofIvy]

Do you even understand what the picture shows you? I'm not sure since you don't try to explain to us what the question is. For example, I can guess that the "m" under each ball is its mass- so that the two balls have the same mass. I can guess that "v_i" and "v_j" are the initial and final velocities of the cue ball and that "v₉" is the velocity of the 9-ball after being hit by the cue ball. It would have been nice if you had said that rather than requiring anyone who wants to help you to guess. And, of course, the only "x" in your picture is the x-axis so "cos(x)" makes no sense at all. I guess you mean $\theta$ but even if you do not know how to make that symbol, it would have been better to type "theta".

You then can use "conservation of momentum". Using v_i, v_f, v₉ now to mean the speed of each ball (magnitude of the velocity vector) the momentum vector of the cue ball before the collision is <mv_i,0>, the momentum vector of the cue ball after the collision is <mv_fcos($\theta$>,mv_fsin($\theta$>, and the momentum vector of the 9-ball after the collision is <mv₉cos(\theta),-mv₉sin(\theta)>. Conservation of momentum gives
<mv_i,0>= <mv_fcos($\theta$>,mv_fsin($\theta$>+ <mv₉cos(\theta),-mv₉sin(\theta)>.

Setting the x-coordinates equal gives mv_i= mv_fcos($\theta$)+ mv₉cos($\theta$). From that equation you get cos($\theta$)= v_i/(v_f+ v₉). Setting the y-coordinates equal gives 0= mv_fsin($\theta$)- mv₉sin($\theta$) or v_f= v₉.
That gives you 2 equations for the 3 unknown values v_f, v₉, and $\theta$ (assuming v_i is given). You can use conservation of kinetic energy to get the third equation.