How Do You Correctly Calculate Tension in a Statics Problem?

[Ortix]

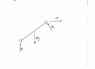
Homework Statement

[PLAIN]http://img830.imageshack.us/img830/1091/unled2cjt.jpg

Homework Equations

I used sum of forces in x y direction and sum of moments

The Attempt at a Solution

So my problem here is that I solved for Ay (1275.3N) and now I have to solve for T

The obvious approach would be to use sum of forces in x direction after doing sum of forces in y to find B. Well I did that and found that B = 2550.6 which is double Ay and equal to mg. B is also perpendicular to the bridge thing. Now when I do sum of forces in x direction i do T = Bcos30 but that's wrong apparently.

Which part am I doing wrong? Is my B wrong?

I calculated B like so:
Fy:0 = Ay - mg + Bsin30

Please help :)

 

[Spinnor]

Does this help? %^)

 

[Ortix]

unfortunately it does not. I figured that much. When i break down the N2 into it's components I still get a wrong answer for T

 

[grzz]

i think that it is important to know whether there is friction with the rollers at A and B.

 

[Ortix]

There is not, so you would think that the x component of the normal force at B would be equal to T, but it's not!

 

[grzz]

If you explain more explicitly how you got B then I can try to give some help.

 

[Ortix]

I calculated B like so:
Fy:0 = Ay - mg + Bsin30

Direct copy from my first post... i don't think i can be more explicit than this..

 

[Spinnor]

There is not, so you would think that the x component of the normal force at B would be equal to T, but it's not!

It has to be. What other forces in the x direction are there?

 

[Ortix]

From what I understand there are 2 forces. B and T both pointing in the opposite direction. Is that correct?

 

[grzz]

I calculated B like so:
Fy:0 = Ay - mg + Bsin30

Direct copy from my first post... i don't think i can be more explicit than this..

I think that sin must be replaced by cos.

 

[grzz]

From what I understand there are 2 forces. B and T both pointing in the opposite direction. Is that correct?

One must be careful here. The SIN30 component of B is in the opposite direction of T.