How Do You Determine Equivalent Capacitance in Complex Circuits?

[jolly_math]

Homework Statement

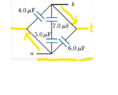
Find the equivalent capacitance between points a and b in the combination of capacitors shown in the figure.

Relevant Equations

parallel: C = C1 + C2 + ...
series: 1/C = 1/C1 + 1/C2 + ...

There are 3 parallel paths: one through 4.0 µF, one through 6.0 µF, and one through 5.0 µF and 7.0 µF.

Why wouldn't there be another path through 4.0 µF, 7.0 µF, 5.0 µF, and 6.0 µF? Also, what determines the direction of current flow when there is a diagonal across parallel paths? Thank you.

 

[gneill]

You can redraw the circuit to make things clearer. The endpoints a and b can be moved anywhere along the lines they connect to, so move them to the bottom and top points as follows:

Then straighten out the bends to make the image more clear:

You should be able to work out the combined capacitance from there?

 

[Nway]

You can redraw the circuit to make things clearer. The endpoints a and b can be moved anywhere along the lines they connect to, so move them to the bottom and top points as follows:
View attachment 320824

Then straighten out the bends to make the image more clear:
View attachment 320825

You should be able to work out the combined capacitance from there?

Sorry please explain @gneill how you got from the top image to the bottom image. I don't see how they are equivalent. Why are you allowed to move the end points a and b around and the diagonal wire in the middle?

 

[robphy]

This might help.

Treat the connecting wire as ideal.
If you take a voltmeter with one probe fixed,
you can move the other probe along the wire of the same color
without changing the voltage reading.

Update: For clarity, I recolored the middle equipotential with a more distinct shade of green
and the bottom equipotential with a more distinct shade of blue.
(It wasn't my intention to shade according to numerical sizes of the potential,
just according to unequal potentials.) Thanks.

Focus on connectivity... not shape or geometry.

 

[kuruman]

The color coding to denote equipotential conductor is nice to show the connectivity, however I think that that the floating piece between the 7.0 μF and 5.0 μF capacitors should be labeled by a different color from the other two because when the capacitors are charged, it will be at an intermediate potential between blue and magenta.

 

[SammyS]

The color coding to denote equipotential conductor is nice to show the connectivity, however I think that that the floating piece between the 7.0 μF and 5.0 μF capacitors should be labeled by a different color from the other two because when the capacitors are charged, it will be at an intermediate potential between blue and magenta.

I think the intermediate wire in @robphy post is green not blue. A rather subtle difference in the two colors .

 

[Nway]

This might help.

Treat the connecting wire as ideal.
If you take a voltmeter with one probe fixed,
you can move the other probe along the wire of the same color
without changing the voltage reading.

Update: For clarity, I recolored the middle equipotential with a more distinct shade of green
and the bottom equipotential with a more distinct shade of blue.
(It wasn't my intention to shade according to numerical sizes of the potential,
just according to unequal potentials.) Thanks.

View attachment 320885View attachment 320886

Focus on connectivity... not shape or geometry.

Sir thank you.