How Do You Determine the Frequency of a Mass Connected to Four Springs?

[Aaron7]

Homework Statement

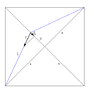
The mass is connected to 4 springs, each connected to a corner of a square with sides √2 a.
The springs have spring constants k and natural length a/2.

Show the frequency of the mass when it is displaced by d << a towards one of the corners is √(3k/m)

Homework Equations

F=kx

The Attempt at a Solution

When in equilibrium the springs are length a.
The forces acting in the same direction of motion would be (a/2 - d)k and -(a/2 + d)k since the spring is already stretch by a/2.

I am having trouble finding the vertical forces acting on the mass by the other 2 springs.
The length of the spring would be stretched to √(a^2 + d^2) so the force would be (√(a^2 + d^2) - a/2)k but I need to find the vertical component of this force.

Working backwards I find that the vertical force on each of the springs must be kd/2 so that (a/2 -d)k - (a/2 +d)k - kd/2 - kd/2 => -3dk so I can move on to use ma = -3xk etc to find the answer. I see a link between being stretched twice its length already and having k/2 but I am not sure why.

Many thanks.

 

[gneill]

When in equilibrium the springs are length a.
The forces acting in the same direction of motion would be (a/2 - d)k and -(a/2 + d)k since the spring is already stretch by a/2.

I am having trouble finding the vertical forces acting on the mass by the other 2 springs.
The length of the spring would be stretched to √(a^2 + d^2) so the force would be (√(a^2 + d^2) - a/2)k but I need to find the vertical component of this force.

Rather than try to find horizontal and vertical components, turn your axes so that one of then runs along the direction of the displacement. You will then be looking for the components of the spring forces along that axis.

You should be able to pick out a triangle similar to (in the geometric sense) the force triangle from which you want to pick out the appropriate component. You will already have the side lengths for this other triangle.

 

[Aaron7]

Ok, so with the triangle with sides a and d, I would work out the force in the d direction by saying:
The force in the a direction is k(a/2) so the force in the d direction is k(d/2) because the distances a and d are similar to the forces acting in the a and d directions. This gets the correct answer. Is this valid reasoning?

 

[gneill]

Ok, so with the triangle with sides a and d, I would work out the force in the d direction by saying:
The force in the a direction is k(a/2) so the force in the d direction is k(d/2) because the distances a and d are similar to the forces acting in the a and d directions. This gets the correct answer. Is this valid reasoning?

Well, something along those lines, but not exactly that. I don't think you can get away from calculating the change in force due to the extension of the springs. However, if you can find the force f when the spring is in its new position, then the component of that force along the line of the displacement can be had by similar triangles.

If L is the length of the spring at its new location, then the total extension of the spring is L - a/2.

In the figure, the ratio f_d/f = d/L holds.

You should be able to determine f from Hook's law and the amount by which L exceeds a/2, the natural length of the spring.

 

[Aaron7]

So I have f=(L- a/2)k

=> f_d = dk(L-a/2) / L
=> f_d = dk - dka/2L

Can I then say cosθ = a/L and since d<<L then cosθ = 1 - θ²/2
so a/L = 1 therefore f_d = dk/2 and then complete it from there?

 

[gneill]

So I have f=(L- a/2)k

=> f_d = dk(L-a/2) / L
=> f_d = dk - dka/2L

Well that looks okay.

Can I then say cosθ = a/L and since d<<L then cosθ = 1 - θ²/2
so a/L = 1 therefore f_d = dk/2 and then complete it from there?

I don't think I'd head off into trig land here. You can find L in terms of a and d, and so f_d likewise.

You've got f_L as the force along the line of a spring as $f_L = k\left(\sqrt{a^2 + d^2} - \frac{a}{2}\right)$ for one spring. Use similar triangles to find the force f_d along the line of displacement. After a bit of simplification you should be able to to see what additional simplification is possible when d << a.