ognik
- 626
- 2
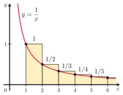
Hi, question asks to set upper and lower bounds on $$\sum_{n=1}^{1,000,000} \frac{1}{n}$$ assuming (a) the Euler-Mascheroni constant is known and (b) not known.
$\gamma = \lim_{{n}\to{\infty\left( \sum_{m=1}^{n} \frac{1}{m} \right)}} = 0.57721566$ and I found (a) easily (14.39272...), but no idea how to approach part b, a hint please?
This is similar to another problem, a pocket calculator gives $ \sum_{1}^{100} \frac{1}{{n}^{-3}}= 1.202 $, find upper and lower limits? Probably the hint will cover both :-)
$\gamma = \lim_{{n}\to{\infty\left( \sum_{m=1}^{n} \frac{1}{m} \right)}} = 0.57721566$ and I found (a) easily (14.39272...), but no idea how to approach part b, a hint please?
This is similar to another problem, a pocket calculator gives $ \sum_{1}^{100} \frac{1}{{n}^{-3}}= 1.202 $, find upper and lower limits? Probably the hint will cover both :-)