ineedhelpnow
- 649
- 0
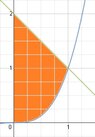
4. find the centroid of the region bounded by the given curves. $y=x^{3}$, $x+y=2$, $x=0$
5. a gate in an irrigation canal is constructed in the form of a trapezoid 3 ft wide at the bottom, 5 ft wide at the top, and 2 ft high. it is placed vertically in the canal, with the water extending to its top. find the hydrostatic force on one side of the gate.
5. a gate in an irrigation canal is constructed in the form of a trapezoid 3 ft wide at the bottom, 5 ft wide at the top, and 2 ft high. it is placed vertically in the canal, with the water extending to its top. find the hydrostatic force on one side of the gate.