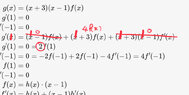How do you find the missing maximum of g(x)?

[lioric]

Homework Statement

g(x) has x intercept x=-3 and x=1
Gradient equal zero at x=1 and x=-1
Find the function g(x)

Relevant Equations

Dy/dx gives the gradient and the second derivative gives the max and min

I’ve found that when I use g(x)= (x+3)(x-1)²
You get everything except the maximum x=-1
I just cannot get that last one

 

[PeroK]

Perhaps you need a 4th or 5th degree polynomial?

 

[fresh_42]

The intercepts only say that $g(x)=(x+3)\cdot (x-1)\cdot f(x)$ for some function $f(x).$ It makes no sense to guess what $f(x)$ might be. What do you get from the second condition?

 

[lioric]

The intercepts only say that $g(x)=(x+3)\cdot (x-1)\cdot f(x)$ for some function $f(x).$ It makes no sense to guess what $f(x)$ might be. What do you get from the second condition?

Second condition?

 

[pasmith]

The zero function g(x) \equiv 0 is a solution. The question then is: are there others?

 

[fresh_42]

Second condition?

Yes, the gradients. Simply differentiate $g'(x)=\left((x+3)(x-1)f(x)\right)'$ and consider the values $g'(1)=g'(-1)=0.$ This gives conditions (intercepts) for $f(x).$ Then proceed by the same way on $f(x).$

 

[lioric]

Yes, the gradients. Simply differentiate $g'(x)=\left((x+3)(x-1)f(x)\right)'$ and consider the values $g'(1)=g'(-1)=0.$ This gives conditions (intercepts) for $f(x).$ Then proceed by the same way on $f(x).$

Ok thank you. I’ll do that. Btw, why are you writing is as (x+3)(x-1)f(x) and not (x+3)(x-1)²?

 

[fresh_42]

Ok thank you. I’ll do that. Btw, why are you writing is as (x+3)(x-1)f(x) and not (x+3)(x-1)²?

I only used the intercepts. They guarantee that $(x-1)\,|\,g(x)$ and $(x+3)\,|\,g(x)$ so $g(x)=(x+3)(x-1)f(x).$ I want to proceed step by step, not all information at once. That led to your wrong guess. $f(x)=(x-1)\cdot h(x)$ drops out of the position all by itself.

... and it was easier to differentiate.

 

[lioric]

Perhaps you need a 4th or 5th degree polynomial?

This helped. I was assuming that it’s still a cubic graph.

 

[lioric]

I multiplied (x+3) to the function and it worked.

 

[lioric]

I only used the intercepts. They guarantee that $(x-1)\,|\,g(x)$ and $(x+3)\,|\,g(x)$ so $g(x)=(x+3)(x-1)f(x).$ I want to proceed step by step, not all information at once. That led to your wrong guess. $f(x)=(x-1)\cdot h(x)$ drops out of the position all by itself.

... and it was easier to differentiate.

I got the answer. (X+3)²(x-1)²
It was a guess cause of the way the question was
But I’d like to know how to do it the was you said.

 

[PeroK]

This helped. I was assuming that it’s still a cubic graph.

I've never worked in maths education, but I'm always surprised at the specific nature of problems. The questions seem to ask you to do some random thing that doesn't really fit into any bigger picture. What is the point of this question? What does it teach you? In what way does it improve your understanding of maths?

What I have always done is try to generalise these problems and understand what is really going on.

First I drew a cubic graph that cuts the x-axis at $x = -3$, has a local maximum somewhere between $x = -3$ and $x = 1$, touches the x-axis at a local minimum at $x = 1$.

My first question is whether this completely specifies the cubic? We know that it must be of the form:
$$g(x) = A(x+3)(x-1)^2$$Note that uses prior knowledge of polynomial roots and turning points. Which you knew, of course.

Now we see that the constant $A$ affects the function value at the local maximum, but that the value of $x$ is determined: the maximum is at $x = -\frac 5 3$. There is no other possibility. I'm not sure how useful that is, but at least I've learned something.

Next we try a quartic equation (4th power). If $g(x)$ is to have precisely two zeroes, then both must also be turning points (local minima). And, again the the function is fully specified. And, the local maximum must be half way between the zeroes (at $x = -1$).

Now, this makes sense. The $x = -1$ was not some random number where we had to arrange a local maximum. The local maximum could only have been at $x = -\frac 5 3$ (when the initial cubic would have worked) or at $x = -1$ (where the quartic worked).

At this stage I think I understand the question fully. I'm still not sure I've learned anything useful for the future, so I'll put that down as a rather pointless exercise, to be honest.

Is it worth thinking about higher order polynomials? Probably not. Time to move on to hopefully more useful problems that provide lasting knowledge!

 

[pasmith]

The conditions on g define a subspace of the space of differentiable functions on [-3,1], so without some further condition there will not be a unique non-zero solution.

 

[fresh_42]

I got the answer. (X+3)²(x-1)²
It was a guess cause of the way the question was
But I’d like to know how to do it the was you said.

I got the same answer. There was a free parameter in my calculation, $A$ in @PeroK 's post #12, $a$ in mine.
\begin{align*}
g(x)&=(x+3)(x-1)f(x)\\
g'(1)&=0\\
g'(-1)&=0\\
g'(x)&=(x-1)f(x)+(x+3)f(x)+(x+3)(x-1)f'(x)\\
g'(1)&=0=2f(1)\\
g'(-1)&=0=-2f(-1)+2f(-1)-4f'(-1)=4f'(-1)\\
f(1)&=0\\
f'(-1)&=0\\
f(x)&=h(x)\cdot (x-1)\\
f'(x)&=h(x)+(x-1)h'(x)\\
f'(-1)&=0=h(-1)-2h'(-1)\\
h'(-1)&=\dfrac{1}{2}h(-1)\\
h(x)&=ax+b\quad\text{ansatz with }a\neq 0\\
h'(x)&=a\\
h'(-1)&=a=\dfrac{1}{2}\left(-a+b\right)=-\dfrac{1}{2}a+\dfrac{1}{2}b\\
a&=\dfrac{1}{3}b\, , \,b=3\, , \,a=1\\
h(x)&=x+3\\
g(x)&=(x+3)^2(x-1)^2=y = x^4 + 4 x^3 - 2 x^2 - 12 x + 9\\
g'(x)&=4x^3+12x^2-4x-12=4(x^3+3x^2-x-3)\\
&=4(x-1)(x+1)(x+3)\quad\text{check}
\end{align*}

 

[Steve4Physics]

FWIW, from inspection $g(x) = \sin(\frac {\pi x}2 ) - 1$ also satisfies the criteria (but, of course, has additional intercepts and points of zero gradient).

 

[lioric]

I've never worked in maths education, but I'm always surprised at the specific nature of problems. The questions seem to ask you to do some random thing that doesn't really fit into any bigger picture. What is the point of this question? What does it teach you? In what way does it improve your understanding of maths?

What I have always done is try to generalise these problems and understand what is really going on.

First I drew a cubic graph that cuts the x-axis at $x = -3$, has a local maximum somewhere between $x = -3$ and $x = 1$, touches the x-axis at a local minimum at $x = 1$.

My first question is whether this completely specifies the cubic? We know that it must be of the form:
$$g(x) = A(x+3)(x-1)^2$$Note that uses prior knowledge of polynomial roots and turning points. Which you knew, of course.

Now we see that the constant $A$ affects the function value at the local maximum, but that the value of $x$ is determined: the maximum is at $x = -\frac 5 3$. There is no other possibility. I'm not sure how useful that is, but at least I've learned something.

Next we try a quartic equation (4th power). If $g(x)$ is to have precisely two zeroes, then both must also be turning points (local minima). And, again the the function is fully specified. And, the local maximum must be half way between the zeroes (at $x = -1$).

Now, this makes sense. The $x = -1$ was not some random number where we had to arrange a local maximum. The local maximum could only have been at $x = -\frac 5 3$ (when the initial cubic would have worked) or at $x = -1$ (where the quartic worked).

At this stage I think I understand the question fully. I'm still not sure I've learned anything useful for the future, so I'll put that down as a rather pointless exercise, to be honest.

Is it worth thinking about higher order polynomials? Probably not. Time to move on to hopefully more useful problems that provide lasting knowledge!

Thank you very much for sharing your insight. Even though this was a waste of time in your opinion, I still value it and you have given me a better understanding of these questions. So please, I value your wisdom greatly

 

[lioric]

I got the same answer. There was a free parameter in my calculation, $A$ in @PeroK 's post #12, $a$ in mine.
\begin{align*}
g(x)&=(x+3)(x-1)f(x)\\
g'(1)&=0\\
g'(-1)&=0\\
g'(x)&=(x-1)f(x)+(x+3)f(x)+(x+3)(x-1)f'(x)\\
g'(1)&=0=2f(1)\\
g'(-1)&=0=-2f(-1)+2f(-1)-4f'(-1)=4f'(-1)\\
f(1)&=0\\
f'(-1)&=0\\
f(x)&=h(x)\cdot (x-1)\\
f'(x)&=h(x)+(x-1)h'(x)\\
f'(-1)&=0=h(-1)-2h'(-1)\\
h'(-1)&=\dfrac{1}{2}h(-1)\\
h(x)&=ax+b\quad\text{ansatz with }a\neq 0\\
h'(x)&=a\\
h'(-1)&=a=\dfrac{1}{2}\left(-a+b\right)=-\dfrac{1}{2}a+\dfrac{1}{2}b\\
a&=\dfrac{1}{3}b\, , \,b=3\, , \,a=1\\
h(x)&=x+3\\
g(x)&=(x+3)^2(x-1)^2=y = x^4 + 4 x^3 - 2 x^2 - 12 x + 9\\
g'(x)&=4x^3+12x^2-4x-12=4(x^3+3x^2-x-3)\\
&=4(x-1)(x+1)(x+3)\quad\text{check}
\end{align*}

This is awesome. I’ll try this out to see if I full understand it, I’ll post if I have doubts. Thank you very much

 

[lioric]

I got the same answer. There was a free parameter in my calculation, $A$ in @PeroK 's post #12, $a$ in mine.
\begin{align*}
g(x)&=(x+3)(x-1)f(x)\\
g'(1)&=0\\
g'(-1)&=0\\
g'(x)&=(x-1)f(x)+(x+3)f(x)+(x+3)(x-1)f'(x)\\
g'(1)&=0=2f(1)\\
g'(-1)&=0=-2f(-1)+2f(-1)-4f'(-1)=4f'(-1)\\
f(1)&=0\\
f'(-1)&=0\\
f(x)&=h(x)\cdot (x-1)\\
f'(x)&=h(x)+(x-1)h'(x)\\
f'(-1)&=0=h(-1)-2h'(-1)\\
h'(-1)&=\dfrac{1}{2}h(-1)\\
h(x)&=ax+b\quad\text{ansatz with }a\neq 0\\
h'(x)&=a\\
h'(-1)&=a=\dfrac{1}{2}\left(-a+b\right)=-\dfrac{1}{2}a+\dfrac{1}{2}b\\
a&=\dfrac{1}{3}b\, , \,b=3\, , \,a=1\\
h(x)&=x+3\\
g(x)&=(x+3)^2(x-1)^2=y = x^4 + 4 x^3 - 2 x^2 - 12 x + 9\\
g'(x)&=4x^3+12x^2-4x-12=4(x^3+3x^2-x-3)\\
&=4(x-1)(x+1)(x+3)\quad\text{check}
\end{align*}

Shouldn’t this be 4f(1) and not 2f(1) ?

 

[fresh_42]

Shouldn’t this be 4f(1) and not 2f(1) ?

Let's see.
\begin{align*}
g'(x)&=(x-1)f(x)+(x+3)f(x)+(x+3)(x-1)f'(x)\\
g'(1)&=0=(1-1)f(1)+(1+3)f(1)+(1+3)(1-1)f'(1)\\
&=4f(1)
\end{align*}
You are right. Good that it was zero anyway, or to say it with Antony Zee:

Yeah, it is reminiscent of what distinguishes the good theorists from the bad ones. The good ones always make an even number of sign errors, and the bad ones always make an odd number.

 

[lioric]

I got the same answer. There was a free parameter in my calculation, $A$ in @PeroK 's post #12, $a$ in mine.
\begin{align*}
g(x)&=(x+3)(x-1)f(x)\\
g'(1)&=0\\
g'(-1)&=0\\
g'(x)&=(x-1)f(x)+(x+3)f(x)+(x+3)(x-1)f'(x)\\
g'(1)&=0=2f(1)\\
g'(-1)&=0=-2f(-1)+2f(-1)-4f'(-1)=4f'(-1)\\
f(1)&=0\\
f'(-1)&=0\\
f(x)&=h(x)\cdot (x-1)\\
f'(x)&=h(x)+(x-1)h'(x)\\
f'(-1)&=0=h(-1)-2h'(-1)\\
h'(-1)&=\dfrac{1}{2}h(-1)\\
h(x)&=ax+b\quad\text{ansatz with }a\neq 0\\
h'(x)&=a\\
h'(-1)&=a=\dfrac{1}{2}\left(-a+b\right)=-\dfrac{1}{2}a+\dfrac{1}{2}b\\
a&=\dfrac{1}{3}b\, , \,b=3\, , \,a=1\\
h(x)&=x+3\\
g(x)&=(x+3)^2(x-1)^2=y = x^4 + 4 x^3 - 2 x^2 - 12 x + 9\\
g'(x)&=4x^3+12x^2-4x-12=4(x^3+3x^2-x-3)\\
&=4(x-1)(x+1)(x+3)\quad\text{check}
\end{align*}

This is just so awesome. Im like, speechless. It’s so elegant. May I please have a one on one class to clarify some doubts? I would be most greatful.

 

[fresh_42]

This is just so awesome. Im like, speechless. It’s so elegant. May I please have a one on one class to clarify some doubts? I would be most greatful.

Have you found my other sign error?

 

[lioric]

Have you found my other sign error?

Yes i did. -4f(x) became a positive.

 

[lioric]

Have you found my other sign error?

As i have asked above, may i have a one on one session with you to clarify some things in what you did here? Its quite interesting.

 

[fresh_42]

As i have asked above, may i have a one on one session with you to clarify some things in what you did here? Its quite interesting.

Why don't you ask here? It would still be on topic and others may profit, too, but, yes, write a PM.

 

[lioric]

Why don't you ask here? It would still be on topic and others may profit, too, but, yes, write a PM.

This is ok, but I’d like to ask the questions and get answers as I am asking them, like a chat. It’s too slow on the forum.

 

[fresh_42]

This is ok, but I’d like to ask the questions and get answers as I am asking them, like a chat. It’s too slow on the forum.

Slow is relative and depends on where on the globe we are. The advantage is that we can write formulas in a reasonable way by using TeX.

 

[lioric]

Slow is relative and depends on where on the globe we are. The advantage is that we can write formulas in a reasonable way by using TeX.

Ok. I’ll ask here the questions may sound a bit stupid, but please humor me. I believe even if it sounds stupid, once it’s explained, stuff becomes clear.

Normally when I differentiate stuff, I need to know the whole function, you differentiated this while part of the function was unknown. I didn’t know you could do that. So this was a new territory.

I’d like to know how your thought process worked to work n a question like this.

 

[fresh_42]

Ok. I’ll ask here the questions may sound a bit stupid, but please humor me. I believe even if it sounds stupid, once it’s explained, stuff becomes clear.

Normally when I differentiate stuff, I need to know the whole function, you differentiated this while part of the function was unknown. I didn’t know you could do that. So this was a new territory.

I’d like to know how your thought process worked to work n a question like this.

Differentiation is a linear operator. That means that $(\alpha\cdot f(x)+\beta\cdot g(x))'=\alpha \cdot f'(x)+ \beta \cdot g'(x)$ with real numbers $\alpha,\beta.$ It uses the properties of differentiation, not the property of functions, except that they are differentiable, of course. The two other important rules are the chain rule $(f(g(x)))'=f'(g(x))\cdot g'(x)$ and the Leibniz or product rule $(f(x)\cdot g(x))'=f'(x)\cdot g(x)+ f(x)\cdot g'(x).$ It is all about $'$ and not about $f$ or $g.$

If you differentiate a polynomial, e.g. $f(x)=4\cdot x^3+7\cdot x-1$ then it is $$
f'(x)=(4\cdot x^3+7\cdot x-1)'=4\cdot (x^3)'+7\cdot (x)'-(1)'=4\cdot (3\cdot x^2)+7\cdot (1) +(0)=12x^2+7$$
so you used the linearity of differentiation.

The other property that I used was, that $x-\alpha$ divides a polynomial $p(x)$ if and only if $p(a)=0.$ You can find the argument for that here:
https://www.physicsforums.com/threads/strange-quadratic-manipulation.1065675/#post-7119262

And finally, I used this ansatz $h(x)=ax+b.$ Of course, I couldn't know whether this was sufficient. If not, I would have used $h(x)=ax^2+bx+c$ instead. But we had only one equation left at this stage of the calculation, so $h(x)=ax+b$ was already one parameter more than necessary, $h(x)=1\cdot x+b$ would have been sufficient. The ansatz $h(x)=b$ would have resulted in the zero function $g(x)\equiv 0$ which is a possible solution, too.

 

[lioric]

Differentiation is a linear operator. That means that $(\alpha\cdot f(x)+\beta\cdot g(x))'=\alpha \cdot f'(x)+ \beta \cdot g'(x)$ with real numbers $\alpha,\beta.$ It uses the properties of differentiation, not the property of functions, except that they are differentiable, of course. The two other important rules are the chain rule $(f(g(x)))'=f'(g(x))\cdot g'(x)$ and the Leibniz or product rule $(f(x)\cdot g(x))'=f'(x)\cdot g(x)+ f(x)\cdot g'(x).$ It is all about $'$ and not about $f$ or $g.$

If you differentiate a polynomial, e.g. $f(x)=4\cdot x^3+7\cdot x-1$ then it is $$
f'(x)=(4\cdot x^3+7\cdot x-1)'=4\cdot (x^3)'+7\cdot (x)'-(1)'=4\cdot (3\cdot x^2)+7\cdot (1) +(0)=12x^2+7$$
so you used the linearity of differentiation.

The other property that I used was, that $x-\alpha$ divides a polynomial $p(x)$ if and only if $p(a)=0.$ You can find the argument for that here:
https://www.physicsforums.com/threads/strange-quadratic-manipulation.1065675/#post-7119262

And finally, I used this ansatz $h(x)=ax+b.$ Of course, I couldn't know whether this was sufficient. If not, I would have used $h(x)=ax^2+bx+c$ instead. But we had only one equation left at this stage of the calculation, so $h(x)=ax+b$ was already one parameter more than necessary, $h(x)=1\cdot x+b$ would have been sufficient. The ansatz $h(x)=b$ would have resulted in the zero function $g(x)\equiv 0$ which is a possible solution, too.

My my my. Such a wonderful explanation. Thank you sir. You’ve made my day