ineedhelpnow
- 649
- 0
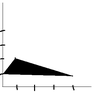
$\int \, \int_{D}^{} \, y^3 dA$ D is the triangular region with vertices (0,1), (1,2), (4,1)
i can't get past this problem. i drew the triangle but i don't know how to find the intervals...
excuse my ugly drawing :p
View attachment 3575
i can't get past this problem. i drew the triangle but i don't know how to find the intervals...
excuse my ugly drawing :p
View attachment 3575