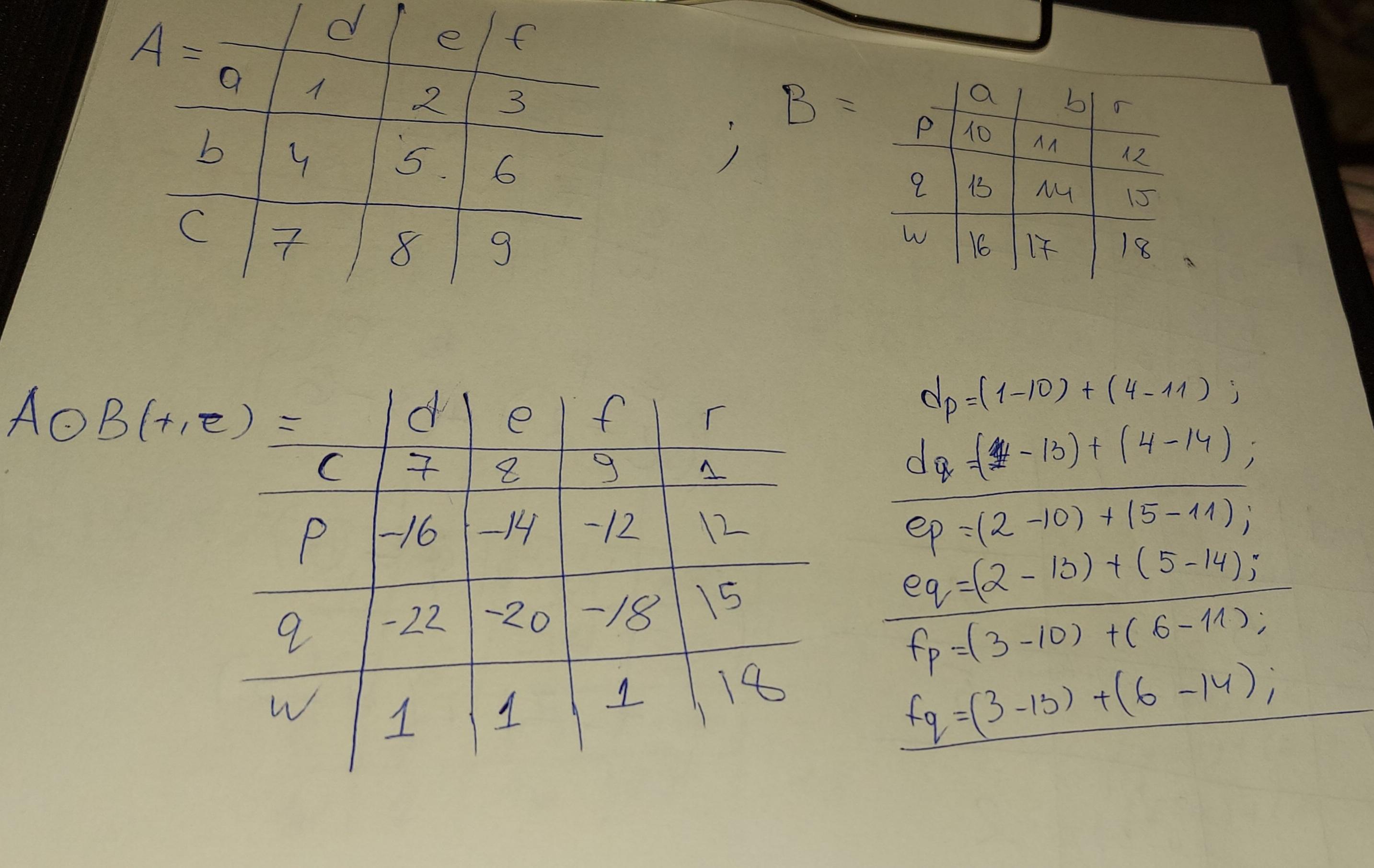
It is extremely difficult to understand what you are writing because you are using a very peculiar notation!
I THINK you mean that
[math]A= \begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \\7 & 8 & 9 \end{pmatrix}[/math]
that
[math]B= \begin{pmatrix}10 & 11 & 12 \\ 13 & 14 & 15 \\ 16 & 17 & 18 \end{pmatrix}[/math]
and you want to find the product
[math]AB= \begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \\7 & 8 & 9 \end{pmatrix}\begin{pmatrix}10 & 11 & 12 \\ 13 & 14 & 15 \\ 16 & 17 & 18 \end{pmatrix}[/math].
One way to think about this is that each row of matrix A is a vector, that each column of matrix B is a vector, and you want to take the "dot product" of the three vectors from A with each of the three vectors from B. (you appear to have labeled row and columns with "p", "q", etc. but that seems to me more complicated and confusing than useful.)
For example, the first row in A is [1, 2. 3] and the first column in B is [10, 13, 16]. Their "dot product" is 1(10)+ 2(13)+ 3(16)= 10+ 26+ 48= 84. The value in the first row, first column of AB is 84.
The first row in A is [1, 2, 3] and the second column in B is [11, 14, 17]. Their "dot product" is 1(11)+ 2(14)+ 3(17)= 11+ 28+ 51= 90. The value in the first row, second column of AB is 90.
The last number in the first row of AB is 1(12)+2(15)+ 3(18)= 12+ 30+ 54= 96. The first row of AB is [math]\begin{pmatrix}84 & 90 & 96\end{pmatrix}[/math].
Do the same but using the second row of A, [math]\begin{pmatrix}4 & 5 & 6 \end{pmatrix}[/math] with the three columns of B to get the second row of AB.
Do the same but using the third row of A, [math]\begin{pmatrix}7 & 8 & 9 \end{pmatrix}[/math] with the three columns of B to get the third row of AB.