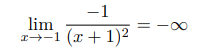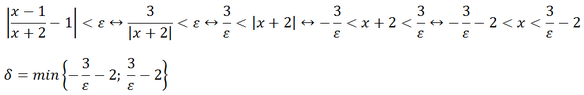goody1
- 16
- 0
Hi, can anybody help me with this two limits? I have to prove them by the definition of limit. Thank you in advance.
View attachment 9630 View attachment 9631
View attachment 9630 View attachment 9631