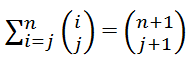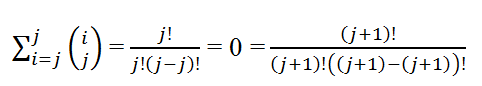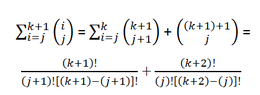How Do You Prove the Formula for n Choose k?

[wittysoup]

Hello all,

I need a little help with how to go about proving the following:
View attachment 619

the formula for n choose k is n!/(k!(n-k)!)

For this, I have proceeded as follows:

Base case P(j):

View attachment 620

I am not sure if this is correct... but the next step would be to Assume P(k), I get stuck at that step because the algebraic expression does not look right... Am I going about this the right way? Thanks.

 

[MarkFL]

Your base case $P_j$ would be:

$\displaystyle \sum_{i=j}^j{i \choose j}={j \choose j}=1={j+1 \choose j+1}$

This is true.

Next, state the induction hypothesis $P_k$:

$\displaystyle \sum_{i=j}^k{i \choose j}={k+1 \choose j+1}$

I think my inductive step would be to add ${k+1 \choose j}$ to both sides:

$\displaystyle \sum_{i=j}^k{i \choose j}+{k+1 \choose j}={k+1 \choose j+1}+{k+1 \choose j}$

$\displaystyle \sum_{i=j}^{k+1}{i \choose j}={k+1 \choose j+1}+{k+1 \choose j}$

Now, what you need to do is show that:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}={(k+1)+1 \choose j+1}$

Essentially, you need to prove Pascal's identity. Use the definition of the binomial coefficients to do so, and if you get stuck, we can offer further guidance.

 

[wittysoup]

Thanks for that, it seems like I miscalculated the first result... I am now stuck here, being that I do not know how to simplify this ( I actually worked out further on paper trying to get a common denominator)...

View attachment 621

 

[MarkFL]

I would state:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}=\frac{(k+1)!}{(j+1)!((k+1)-(j+1))!}+\frac{(k+1)!}{j!((k+1)-j)!}$

Simplify a bit:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}=\frac{(k+1)!}{(j+1)!(k-j)!}+\frac{(k+1)!}{j!(k+1-j)!}$

Next, factor:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}=\frac{(k+1)!}{j!(k-j)!}\left(\frac{1}{j+1}+\frac{1}{k+1-j} \right)$

Combine terms within parentheses:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}=\frac{(k+1)!}{j!(k-j)!}\left(\frac{k+1-j+j+1}{(j+1)(k+1-j)} \right)$

Combine like terms:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}=\frac{(k+1)!}{j!(k-j)!}\left(\frac{k+2}{(j+1)(k+1-j)} \right)$

Combine factors:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}=\frac{(k+2)!}{(j+1)!(k+1-j)!}$

Rewrite right side as binomial coefficient:

$\displaystyle {k+1 \choose j+1}+{k+1 \choose j}={(k+1)+1 \choose j+1}$

Thus, using this result in our inductive step, we obtain:

$\displaystyle \sum_{i=j}^{k+1}{i \choose j}={(k+1)+1 \choose j+1}$

We have derived $P_{k+1}$ from $P_k$ thereby completing the proof by induction.

 

[blue_raver22]

Hello,

Thank you for reaching out for help with proving the formula for n choose k. Your approach so far is on the right track, but there are a few things that can be improved.

First, let's define what n choose k means. It represents the number of ways to choose k objects from a set of n objects, without regard to the order in which they are chosen. So, for example, if we have a set of 5 objects and we want to choose 3 of them, n choose k would give us the number of possible combinations of 3 objects from the set of 5.

With that in mind, let's start with the base case P(j). This should be the simplest case where n choose k is easy to calculate. In this case, we can choose all n objects from the set, which means n choose n = 1. This is because there is only one way to choose all n objects - by choosing all of them.

Next, we can move on to the inductive step, where we assume P(k) and try to prove P(k+1). This means we are assuming that the formula holds for choosing k objects from a set of n objects, and we want to show that it also holds for choosing k+1 objects from a set of n+1 objects.

To do this, we can use the fact that n choose k can also be written as n choose (n-k). This is because choosing k objects from a set of n is the same as choosing n-k objects to not be included in the chosen set. So, we can rewrite the formula as n choose (n-k) = n!/(k!(n-k)!).

Next, we can use the definition of n choose k to expand the left side of the equation. This gives us (n+1) choose (k+1) = (n+1)!/((k+1)!(n+1-k)!).

Now, we can use the inductive hypothesis that P(k) is true, which means n choose k = n!/(k!(n-k)!). We can substitute this into our expanded equation, giving us (n+1)!/((k+1)!(n+1-k)!) = (n!/(k!(n-k)!))*(n+1)/((k+1)(n+1-k)).

From here, we can simplify the expression by cancelling out common terms and rearranging