How Do You Sketch Position and Tangent Vectors for a Vector Function?

[ineedhelpnow]

$r(t)=\left\langle t-2, t^2+1 \right\rangle$, $t=-1$

sketch the plane curve with the given vector equation.

$x=t-2$ and $y=t^2+1$

$x+2=t$
$(x+2)^2=t^2$
$(x+2)^2+1=t^2+1$
$(x+2)^2+1=y$
$x^2+4x+4+1=y$
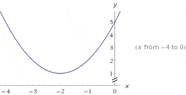
$y=x^2+4x+5$ it's a parabola

View attachment 3099find $r'(t)$

$r'(t)=\left\langle 1, 2t \right\rangle$

sketch the position vector $r(t)$ and the tangent vector $r'(t)$ for the given value of $t$ (this is the part I am having trouble with)

when $t=-1$
$r(-1)=\left\langle -3, 2 \right\rangle$
$r'(-1)=\left\langle 1, -2 \right\rangle$

how do i sketch the position vectors?

 

[I like Serena]

View attachment 3099
sketch the position vector $r(t)$ and the tangent vector $r'(t)$ for the given value of $t$ (this is the part I am having trouble with)
when $t=-1$
$r(-1)=\left\langle -3, 2 \right\rangle$
$r'(-1)=\left\langle 1, -2 \right\rangle$

how do i sketch the position vectors?

Hey ineedhelpnow! ;)

The position vector is a vector from the origin (0,0) to the point (-3,2).
The tangent vector is a vector from the point (-3,2) to (-3,2)+(1,-2)=(-2,0).

Care to draw those 2 vectors? (Wondering)

 

[ineedhelpnow]

hey.

YES! thanks sooo much.