ashley2024
- 5
- 0
- Homework Statement
- Find the tension in the following system (see image).
- Relevant Equations
- Fnet = ma, Ff = uFn,
Please note that the system is not in equilibrium, and that tension must be solved for the instant where the angle is 154 degrees.

My attempt (correct ans is Ft = 626N)
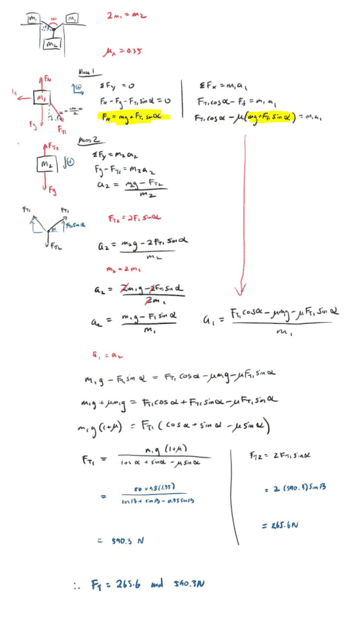
My attempt (correct ans is Ft = 626N)