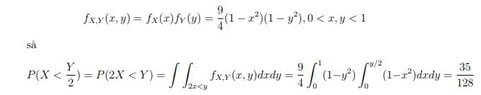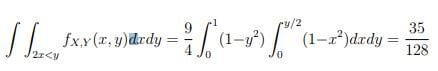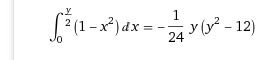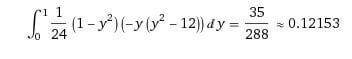How Do You Solve an Integral with Two Variables?

[goohu]

Hey there, trying to figure out how to solve this integral (see picture).

View attachment 8728

I've never seen an integral written in this way before.

I've tried to integrate the x-part first and then the y-part and vice versa but they both gave the wrong results.

 

[HOI]

First \int_0^{y/2} (1- x^2) dx= \left[x- \frac{x^3}{3}\right]_0^{y/2}= \frac{y}{2}- \frac{1}{3}\frac{y^3}{8}

Then \int_0^1 (1- y^2)(\frac{y}{2}- \frac{y^3}{24} dy= \int_0^1 \frac{y}{2}- \frac{13y^3}{24}+ \frac{y^5}{24} dy= \left[\frac{y^2}{4}- \frac{13y^4}{96}+ \frac{y^6}{144}\right]_0^1= \frac{1}{4}- \frac{13}{96}+ \frac{1}{144}= \frac{72+ 39+ 2}{288}= \frac{113}{288}.

Finally, \frac{9}{4}\frac{113}{288}= \frac{113}{128}.
(Check my arithmetic.)

 

[goohu]

thanks for the quick reply. I re-did your calculations and get the same results as you. After using wolfram alpha (online calculator) i get different results though:

first step:
View attachment 8730

second step:
View attachment 8731

(35/288)*(9/4) = 35/128 = correct answer.

This is weird and its bugging me. Are the hand calculation wrong somewhere?

 

[topsquark]

thanks for the quick reply. I re-did your calculations and get the same results as you. After using wolfram alpha (online calculator) i get different results though:

first step:second step:(35/288)*(9/4) = 35/128 = correct answer.

This is weird and its bugging me. Are the hand calculation wrong somewhere?

That's why I deleted my post in this thread. I can't find an error in Country Boy's result, which is essentially identical to my own. I can't explain why the two are different.

-Dan

 

[I like Serena]

thanks for the quick reply. I re-did your calculations and get the same results as you. After using wolfram alpha (online calculator) i get different results though:

first step:second step:(35/288)*(9/4) = 35/128 = correct answer.

This is weird and its bugging me. Are the hand calculation wrong somewhere?

\ldots = \frac{1}{4}- \frac{13}{96}+ \frac{1}{144}= \frac{72+ 39+ 2}{288}= \frac{113}{288}

It's a plus-and-minus thing.
It should be \frac{1}{4}- \frac{13}{96}+ \frac{1}{144}= \frac{72 {\color{red}-} 39+ 2}{288}= \frac{35}{288}

 

[goohu]

Spoiler

heh found it.

$$\displaystyle \frac{1}{4}-\frac{13}{96}+\frac{1}{144} = \frac{72-39+2}{288}$$

while i was figuring out how to post equations klaas beat me to it. Cheers anyways!